Bài 4 trang 40 SGK Hình học 10

Đề bài

 Chứng minh rằng với mọi góc \(α \, \,  (0^0≤ α ≤ 180^0)\) ta đều có \(si{n^2}\alpha  + {\cos ^2}\alpha  = 1.\)

Hướng dẫn giải

+) Sử dụng định lý Pi-ta-go và các công thức lượng giác của góc nhọn cơ bản.

Lời giải chi tiết

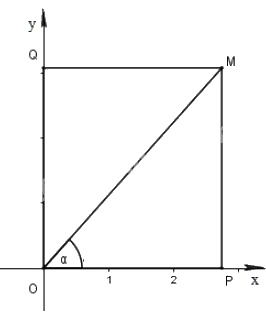
Từ \(M\) kẻ \(MP ⊥ Ox\), \(MQ ⊥ Oy\)

Xét tam giác vuông \(OMP\) có:

\(sin\alpha  = {{MP} \over {OM}}; \, \, \cos \alpha  = {{OP} \over {OM}}. \)

\(\Rightarrow {\sin ^2}\alpha  + {\cos ^2}\alpha  = {{M{P^2} + O{P^2}} \over {O{M^2}}} = {{O{M^2}} \over {O{M^2}}}\)\( = 1.\)