Trang chủ
Lớp 10
Toán Lớp 10 SGK Cũ
Bài 3. Các hệ thức lượng trong tam giác và giải tam giác
Bài 9 trang 59 SGK Hình học 10
Bài 9 trang 59 SGK Hình học 10
Lý thuyết
Bài tập
Mục lục
Tóm tắt bài
Đề bài
Cho hình bình hành \(ABCD\) có \(AB = a, BC = b ,BD = m\), và \(AC = n\). Chứng minh rằng :
$${m^2} + {n^2} = 2({a^2} + {b^2})$$
Hướng dẫn giải
+) Công thức đường trung tuyến: \( m_a^2= {{{b^2} + {c^2}} \over 2} - {{{a^2}} \over 4}=\frac{2(b^2+c^2)-a^2}{4}.\)
Lời giải chi tiết
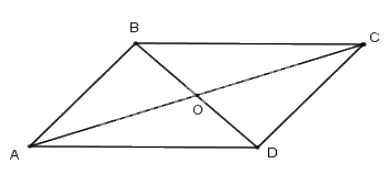
Gọi O là giao điểm của AC và BD. Khi đó O là trung điểm của AC và BD.
Áp dụng định lí về đường trung tuyến:
\(OA^2 =\frac{AD^{2}+AB ^{2}}{2} - \frac{BD^{2}}{4}\)
Thay \(OA = \frac{n}{2}, \, AB = a,\) \(AD = BC = b\) và \(BD = m\) ta được:
\({\left( {{n \over 2}} \right)^2} = {{{b^2} + {a^2}} \over 2} - {{{m^2}} \over 4} \)\(\Rightarrow {n^2} = 2{b^2} + 2{a^2} - {m^2} \)
\(\Rightarrow {m^2} + {n^2} = 2({a^2} + {b^2}).\)
Copyright © 2021 HOCTAP247
