Bài 4 trang 53 SGK Hình học 11

Đề bài

Cho bốn điểm \(A, B, C\) và \(D\) không đồng phẳng.  Gọi \({G_{A}}^{}\), \({G_{B}}^{}\), \({G_{C},{G_{D}}^{}}^{}\) lần lượt là trọng tâm của tam giác \(BCD, CDA, ABD, ABC\). Chứng minh rằng, \(A{G_{A},B{G_{B},C{G_{C},D{G_{D}}^{}}^{}}^{}}^{}\) đồng quy.

Hướng dẫn giải

Gọi \(G = A{G_A} \cap B{G_B};\,\,G' = A{G_A} \cap C{G_C};\) \(G'' = A{G_A} \cap D{G_D}\), chứng minh các tỉ số \(\frac{{GA}}{{G{G_A}}} = \frac{{G'A}}{{G'{G_A}}} = \frac{{G''A}}{{G''{G_A}}} \Rightarrow G \equiv G' \equiv G''\).

Lời giải chi tiết

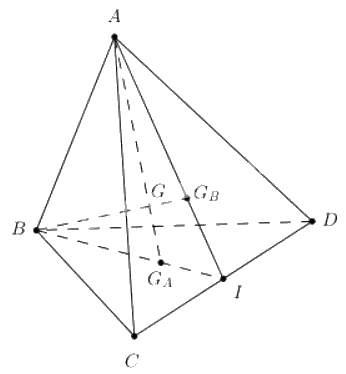
Gọi \(I\) là trung điểm của \(CD\). Ta có \( G_{A}\in BI, {G_{B}}\in AI\).

Trong \((ABI)\) gọi  \( G = A{G_{A}}\)\( \cap B{G_{B}}^{}\).

Dễ thấy \( \frac{I{G_{A}}^{}}{IB}\) = \( \frac{I{G_{B}}^{}}{IA} = \frac{1}{3}\) nên \({G_{A}}^{}\) \({G_{B}}^{} // AB\) và \( \frac{GA}{G{G_{A}}^{}}\) = \( \frac{AB}{{G_{A}{G_{B}}^{}}^{}}\) = 3

Gọi \(G' = A{G_A} \cap C{G_C};\,\,G'' = A{G_A} \cap D{G_D}\).

Chứng minh tương tự ta có \(\frac{{G'A}}{{G'{G_A}}} = \frac{{G''A}}{{G''{G_A}}} = 3\)

Vậy \(G ≡ G' ≡ G''\).