Bài 7 trang 92 SGK Hình học 11
Tóm tắt bài
Đề bài
Gọi \(M\) và \(N\) lần lượt là trung điểm của các cạnh \(AC\) và \(BD\) của tứ diện \(ABCD\). Gọi \(I\) là trung điểm của đoạn thẳng \(MN\) và \(P\) là một điểm bất kì trong không gian. Chứng minh rằng:
a) \(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=\overrightarrow{0};\)
b) \(\overrightarrow{PI}=\frac{1}{4}(\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}+\overrightarrow{PD}).\)
Hướng dẫn giải
a) Sử dụng công thức \(\overrightarrow {MA} + \overrightarrow {MB} = 2\overrightarrow {MI} \) với \(M\) là điểm nằm ngoài đoạn thẳng \(AB\) và \(I\) là trung điểm của \(AB\).
b) Sử dụng quy tắc ba điểm.
Lời giải chi tiết
a) \(\overrightarrow{IA}+\overrightarrow{IB}=2\overrightarrow{IM},\) (Vì M là trung điểm của AB)
\(\overrightarrow{IC}+\overrightarrow{ID}=2\overrightarrow{IN}.\) (Vì N là trung điểm của CD)
Cộng từng vế ta được :
\(\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} + \overrightarrow {ID} = 2\left( {\overrightarrow {IM} + \overrightarrow {IN} } \right) = \overrightarrow 0 \)
b)
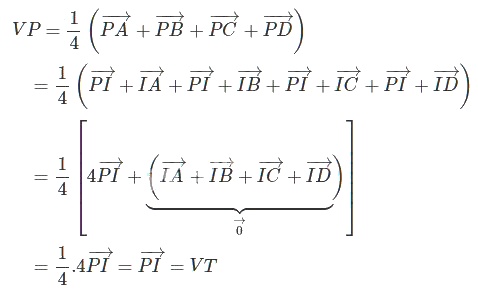
Copyright © 2021 HOCTAP247
