Bài 12 trang 21 SGK Vật lí 11

Đề bài

Hai điện tích điểm q₁ = 3.10^-8 C và q₂  = - 4.10^-8 C đặt cách nhau 10 cm trong chân không. Hãy tìm các điểm mà tại đó cường độ điện trường bằng không. Tại các điểm đó có điện trường không?

Hướng dẫn giải

+ Cường độ điện trường của một điện tích điểm trong chân không: \(E = k{{\left| Q \right|} \over {{r^2}}}\)

+ Vecto cường độ điện trường \(\overrightarrow E \) của điện trường tổng hợp: \(\overrightarrow E  = \overrightarrow {{E_1}}  + \overrightarrow {{E_2}} \)

Lời giải chi tiết

- Điện tích điểm q₁ = 3.10^-8 C đặt tại điểm A, q₂  = - 4.10^-8 C đặt tại điểm B, AB = 10cm.

- Gọi C là điểm mà tại đó cường độ điện trường bằng không.

- Gọi \(\overrightarrow{E_{1C}}\) và \(\overrightarrow{E_{2C}}\)  là cường độ điện trường của q₁ và q₂ tại C.

- Cường độ điện trường tổng hợp tại C:

\(\overrightarrow {{E_C}}  = \overrightarrow {{E_{1C}}}  + \overrightarrow {{E_{2C}}}  = 0 \Rightarrow \overrightarrow {{E_{1C}}}  =  - \overrightarrow {{E_{2C}}} \)

=>Hai vecto này cùng phương, ngược chiều, cùng độ lớn.

 + Hai vecto cùng phương, tức là điểm C phải nằm trên đường thẳng AB.

 + Hai vectơ này phải ngược chiều, tức là C phải nằm ngoài đoạn AB.

 + Hai vectơ này có cùng độ lớn, tức là điểm C gần A hơn B vì |q₁| 2|.

Ta có hình vẽ:

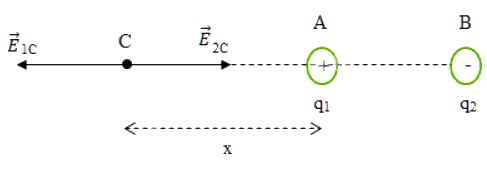
Đặt AC = x, ta có :

\(\eqalign{
& {E_{1C}} = {E_{2C}} \Leftrightarrow k{{\left| {{q_1}} \right|} \over {{x^2}}} = k{{\left| {{q_2}} \right|} \over {{{\left( {AB + x} \right)}^2}}}\cr& \Rightarrow {{{{\left( {AB + x} \right)}^2}} \over {{x^2}}} = \left| {{{{q_2}} \over {{q_1}}}} \right| \Leftrightarrow {{{{\left( {10 + x} \right)}^2}} \over {{x^2}}} = {4 \over 3} \cr
& \Leftrightarrow {{100 + 20x + {x^2}} \over {{x^2}}} = {4 \over 3}\cr& \Rightarrow {x^2} - 60x - 300 = 0 \cr&\Rightarrow \left[ \matrix{
x = 64,6 \hfill \cr
x = - 4,6 \hfill \cr} \right. \Rightarrow AC = 64,6cm \cr} \)

- Ngoài ra còn phải kể đến các điểm nằm rất xa q₁ và q₂. Tại điểm C và các điểm này thì cường độ điện trường cũng bằng không, tức là không có điện trường.