Bài 13 trang 21 SGK Vật lí 11
Tóm tắt bài
Đề bài
Tại hai điện tích điểm A và B cách nhau 5cm trong chân không có hai điện tích q1 = +16.10-8 C và q2 = - 9.10-8 C. Tính cường độ điện trường tổng hợp và vẽ vectơ cường độ điện trường tại điểm C nằm cách A một khoảng 4cm và cách B một khoảng 3cm.
Hướng dẫn giải
+ Cường độ điện trường của một điện tích điểm trong chân không: \(E = k{{\left| Q \right|} \over {{r^2}}}\)
+ Vecto cường độ điện trường \(\overrightarrow E \) của điện trường tổng hợp: \(\overrightarrow E = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} \)
Lời giải chi tiết
Gọi \(\overrightarrow{E_{1}}\) và \(\overrightarrow{E_{2}}\) lần lượt là cường độ điện trường do q1 và q2 gây ra ở C.
Do AB = 5cm; AC = 4cm; BC = 3cm => tam giác ABC vuông tại C.
Cường độ điện trường tổng hợp tại C: \(\overrightarrow {{E_C}} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} \)
Ta có hình vẽ:
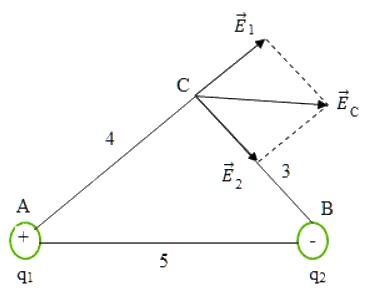
Ta có:
\({E_1} = k{{\left| {{q_1}} \right|} \over {A{C^2}}} = {{{{9.10}^9}.\left| {{{16.10}^{ - 8}}} \right|} \over {{{\left( {{{4.10}^{ - 2}}} \right)}^2}}} = {9.10^5}V/m\)
\({E_2} = k{{\left| {{q_2}} \right|} \over {B{C^2}}} = {{{{9.10}^9}.\left| { - {{9.10}^{ - 8}}} \right|} \over {{{\left( {{{3.10}^{ - 2}}} \right)}^2}}} = {9.10^5}V/m\)
Vì tam giác ABC vuông tại C nên hai vectơ \(\overrightarrow{E_{1}}\) và \(\overrightarrow{E_{2}}\) vuông góc với nhau.
=> Cường độ điện trường tổng hợp tại C là:
\(\left\{ \matrix{
{E_C} = \sqrt {E_1^2 + E_2^2} \hfill \cr
{E_1} = {E_2} \hfill \cr} \right. \)
\(\Rightarrow {E_C} = \sqrt 2 {E_1} = \sqrt 2 {.9.10^5} = {12,7.10^5}\left( {V/m} \right)\)
Copyright © 2021 HOCTAP247
