Giải câu 2 trang 23- Sách giáo khoa Vật lí 9

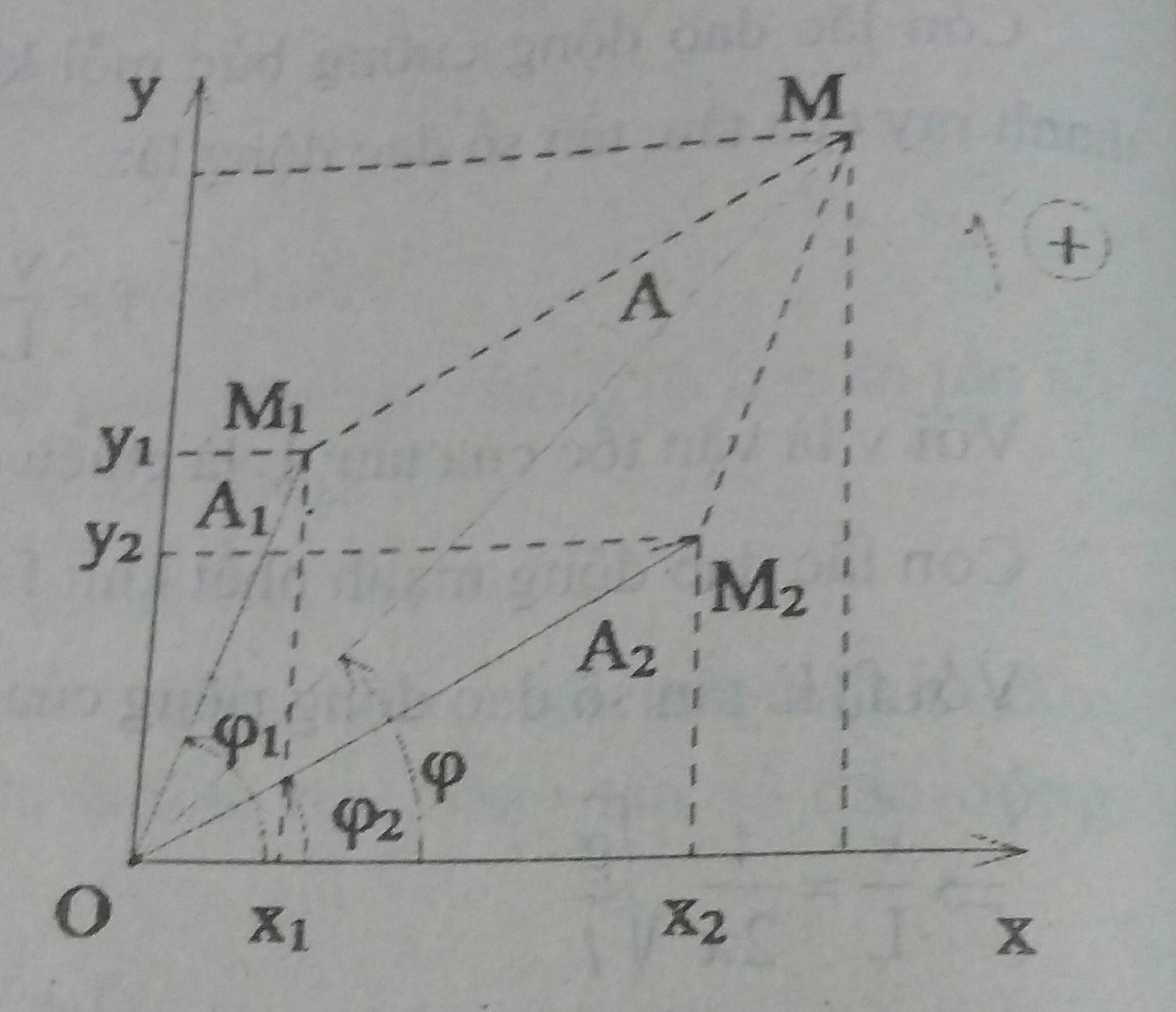
 Áp dụng định lí hàm số côsin, được:

   \(A^2=A_1^2+A_2^2-2A_1A_2cos[\pi - (\varphi_2-\varphi_1)]=A_1^2+A_2^2+2A_1A_2cos(\varphi_2-\varphi_1)\)

  Có: \(\vec{A}=\vec{A_1}+\vec{A_2}\) (1)

   Chiếu (1) lên trục Ox được:

   \( Acos \varphi= A_1cos \varphi_1+ A_2cos \varphi_2\)   (1)

Chiếu trục (1) lên trục Ox, được:

   \( Asin \varphi= A_1sin \varphi_1+ A_2sin \varphi_2\)   (3)

  Chia vế của (3) cho (2) được:

   \(tan \varphi =\dfrac{ A_1sin \varphi_1+ A_2sin \varphi_2}{A_1cos \varphi_1+ A_2cos\varphi_2}\)