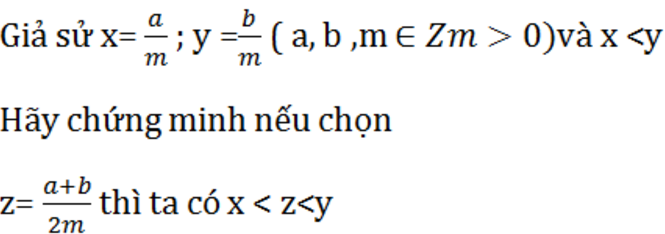Giải bài 5 trang 8 - Sách giáo khoa Toán 7 tập 1

Đề bài

Hướng dẫn giải

Ta có :

x = \(\dfrac{a}{m}\) ; y = \(\dfrac{b}{m}\) ( Với a,b,m \(\in\) Z, m > 0 )

Và x < y

Do đó a <b , suy ra : am < bm

• Ta chứng minh x < z hay \(\dfrac{a}{m}\) < \(\dfrac{a+b}{2m}\)

Ta có :  

  am < bm \(\Rightarrow\) am + am < bm + am ( cộng hai vế với am )

                 \(\Rightarrow\) 2am < (a+b)m \(\Rightarrow\) a < \(\dfrac{(a+b)m}{2m}\)

                 \(\Rightarrow\) \(\dfrac{a}{m}\) < \(\dfrac{a+b}{2m}\) ( chia hai vế cho m > 0 )

Vậy x < z (1)

• Ta chứng minh z < y hay \(\dfrac{a+b}{2m}\) < \(\dfrac{b}{m}\)

Ta có : 

  am < bm \(\Rightarrow\) am + bm < bm + bm ( cộng hai vế với bm )

                 \(\Rightarrow\) (a + b)m < 2bm

                 \(\Rightarrow\) \(\dfrac{a+b}{2m}\) < \(\dfrac{b}{m}\) ( chia hai vế cho \(2m^2\) )

Hay z < y (2)

Từ (1) và (2) suy ra : x < z < y