Giải bài 9 Trang 189 - Sách giáo khoa Vật lí 11
Tóm tắt bài
a) Vẽ hình:
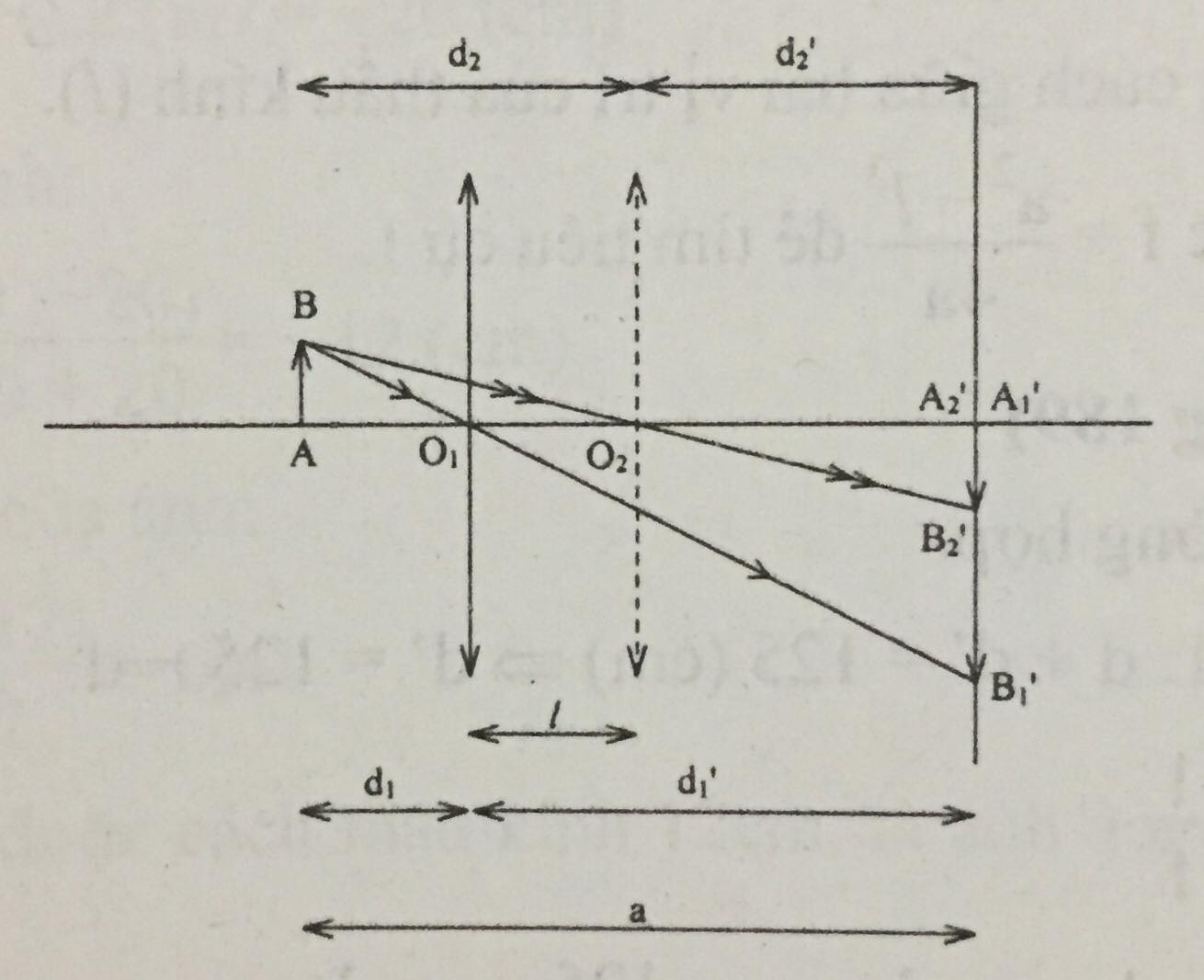
\(d_1=\overline{O_1A}; d_1'=\overline{O_1A_1'}A'_1\)
\(d_2=\overline{O_2A}; d_2'=\overline{O_2A_2'}\)
\(l=O_1O_2;a=AA_1\)
Ta có: \(\dfrac{1}{d_1}+\dfrac{1}{d_1'}=\dfrac{1}{f_1};d_1+d_1'=a\)
Theo tính thuận nghịch của chiều truyền ánh sáng, nếu \(A_1'B_1'\) là vật thì AB là ảnh, nên: \(d_2=d_1'; d_2'=d_1\)
Vậy vị trí thứ hai của thấu kính cách vật một đoạn bằng \(d_1'\).
b) Từ lập luận câu a, ta có:
\(d_1'+d_1=a\) (1)
Lại có \(d_2-d_1=l \Rightarrow d_1'-d_1=l\) (2)
Từ (1) và (2) suy ra: \(d_1'=\dfrac{l+a}{2};d_1=\dfrac{a-l}{2}\)
Tiêu cự của thấu kính:
\(f=\dfrac{d_1d_1'}{d_1+d_1'}=\dfrac{\left (\dfrac{l+a}{2} \right )\left (\dfrac{a-l}{2} \right )}{a}=\dfrac{a^2-l^2}{4a}\)
Vậy, \(f=\dfrac{a^2-l^2}{4a}\)
Muốn tìm tiêu cự của thấu kính ta dùng thí nghiệm để tìm được hai vị trí của thấu kính cho ảnh rõ nét trên màn:
- Đo khoảng cách từ vật tới màn (a).
- Đo khoảng cách giữa hai vị trí của thấu kính (l).
Dùng hệ thức \(f=\dfrac{a^2-l^2}{4a}\) để tìm tiêu cự f.
Copyright © 2021 HOCTAP247
