Hình học 8 Bài 3: Diện tích tam giác

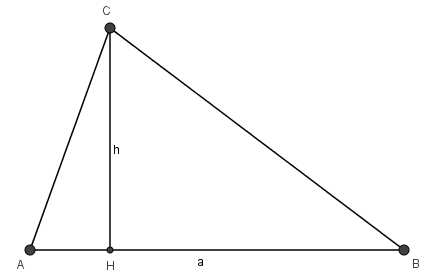
Diện tích tam giác bằng nửa tích của một cạnh với chiều cao ứng với cạnh đó.

\({\rm{S = }}\frac{1}{2}{ah}\)
 

 

Diện tích tam giác vuông bằng nửa tích hai cạnh góc vuông.

\({\rm{S = }}\frac{1}{2}{bc}\)

Bài 1: Cho tam giác đều ABC có cạnh là a, I là một điểm di động thuộc miền trong của tam giác. gọi M;N;P lần lượt là hình chiếu của I lên AB,BC,AC. CHứng minh rằng khi I di chuyển trOng tam giác thì tổng IM+IN+IP không đổi.

Hướng dẫn:

Ta có:

\(\begin{array}{l} {S_{ABC}} = {S_{AIB}} + {S_{BIC}} + {S_{AIC}}\\ = \frac{1}{2}a.IM + \frac{1}{2}a.IN + \frac{1}{2}a.IP\\ = \frac{1}{2}a.\left( {IM + IN + IP} \right)\\ \Rightarrow IM + IN + IP = \frac{{2{S_{ABC}}}}{a} \end{array}\)

Mà tam giác ABC cố định và a cố định nên tổng IM+IN+IP không đổi khi I thay đổi.

Bài 2: Cho tam giác ABC trung tuyến AM. Qua B kẻ đường thẳng song song với AM cắt CA tại E. Gọi I là giao điểm của EM với AB. Chứng minh rằng các cặp tam giác sau có cùng diện tích: ABC và MEC; IEA và IMB

Hướng dẫn:

 

AM song song với BE

\( \Rightarrow {d_{\left( {A,BE} \right)}} = {d_{\left( {M,BE} \right)}}\)

\( \Rightarrow \frac{1}{2}BE.{d_{\left( {A,BE} \right)}} = \frac{1}{2}BE.{d_{\left( {M,BE} \right)}}\) (nhân cả hai vế cho \(\frac{1}{2}BE\))

\( \Rightarrow {S_{ABE}} = {S_{MBE}}\)

\( \Rightarrow {S_{BEC}} - {S_{ABE}} = {S_{BEC}} - {S_{MBE}}\)

\( \Rightarrow {S_{ABC}} = {S_{MEC}}\)

\(\begin{array}{l} \Rightarrow {S_{ABM}} + {S_{AMC}} = {S_{MEA}} + {S_{AMC}}\\ \Rightarrow {S_{ABM}} = {S_{MEA}}\\ \Rightarrow {S_{IBM}} + {S_{IAM}} = {S_{IE{\rm{A}}}} + {S_{IAM}}\\ \Rightarrow {S_{IBM}} = {S_{IE{\rm{A}}}} \end{array}\)

Bài 3: Cho tam giác ABC vuông cân tại A có cạnh AB=6cm, trên đoạn AB, AC lần lượt lấy M và N sao cho AM=CN. Tính AM sao cho diện tích tam giác AMN lớn nhất 

Hướng dẫn:

Gọi độ dài AM là x (0

Diện tích tam giác AMN là :

\(\begin{array}{l} {S_{AMN}} = \frac{1}{2}AM.AN\\ = \frac{1}{2}x.\left( {6 - x} \right) = \frac{1}{2}\left( { - {x^2} + 6{\rm{x}}} \right) \end{array}\)

diện tích AMN lớn nhất khi \( - {x^2} + 6{\rm{x}}\) lớn nhất. Ta có:

\(\begin{array}{l} - {x^2} + 6{\rm{x = }} - {x^2} + 6{\rm{x}} - 9 + 9\\ = - {\left( {x - 3} \right)^2} + 9 \le 9 \end{array}\)

dấu "=" xảy ra khi \({x - 3}\)=0  tức là x=3.

Vậy tam giác AMN có diện tích lớn nhất khi  AM=3 cm.

 

 

Qua bài giảng Diện tích tam giác này, các em cần hoàn thành 1 số mục tiêu mà bài đưa ra như : 

• Nắm vững công thức tính diện tích tam giác, diện tích tam giác vuông

Các em có thể hệ thống lại nội dung kiến thức đã học được thông qua bài kiểm tra Trắc nghiệm Hình học 8 Bài 3 cực hay có đáp án và lời giải chi tiết. 

Câu 2- Câu 5: Xem thêm phần trắc nghiệm để làm thử Online 

Bài tập 24 trang 123 SGK Toán 8 Tập 1

Bài tập 25 trang 123 SGK Toán 8 Tập 1

Bài tập 25 trang 159 SBT Toán 8 Tập 1

Bài tập 26 trang 159 SBT Toán 8 Tập 1

Bài tập 27 trang 159 SBT Toán 8 Tập 1

Bài tập 28 trang 160 SBT Toán 8 Tập 1

Bài tập 29 trang 160 SBT Toán 8 Tập 1

Bài tập 30 trang 160 SBT Toán 8 Tập 1

Bài tập 31 trang 160 SBT Toán 8 Tập 1

Bài tập 31 trang 160 SBT Toán 8 Tập 1

Bài tập 3.2 trang 161 SBT Toán 8 Tập 1

Bài tập 3.3 trang 161 SBT Toán 8 Tập 1

Trong quá trình học tập nếu có thắc mắc hay cần trợ giúp gì thì các em hãy comment ở mục Hỏi đáp, Cộng đồng Toán HOC247 sẽ hỗ trợ cho các em một cách nhanh chóng!

Chúc các em học tập tốt và luôn đạt thành tích cao trong học tập!