Hình học 11 Bài 1: Vectơ trong không gian
Tóm tắt bài
1.1. Các phép tính vectơ
a) Quy tắc hình bình hành
Nếu ABCD là hình bình hành thì: \(\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD}.\)
b) Quy tắc ba điểm đối với phép cộng vectơ
Cho ba điểm A, B, C bất kì thì \(\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {BC}\).
(1).png)
Quy tắc ba điểm với phép trừ vectơ: \(\overrightarrow {AB} = \overrightarrow {OB} - \overrightarrow {OA} ..\)
c) Quy tắc hình hộp
Cho hình hộp ABCD. A’B’C’D’ thì \(\overrightarrow {AC'} = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {{\rm{AA'}}}\).
d. Quy tắc nhận vectơ với một số:
Cho vectơ \(\vec a\) và một số thực \(k \ne 0\) ta được vectơ \(k \vec a\) có các tính chất sau:
- \(\left| {k.\overrightarrow a } \right| = \left| k \right|.\left| {\overrightarrow a } \right|{\rm{ }}\).
- Nếu k>0 thì \(\vec a\) cùng hướng với \(k \vec a\).
- Nếu k<0 thì \(k \vec a\) ngược hướng với \(k \vec a\).
1.2. Điều kiện đồng phẳng của ba vectơ
a) Vectơ cùng phương
Điều kiện cần và đủ để hai vectơ \(\vec a, \vec b\)cùng phương là có một số thực k để \(\overrightarrow a = k.\overrightarrow b.\)
b) Vectơ đồng phẳng
- Trong không gian ba vectơ được gọi là đồng phẳng nếu các giá của chúng cùng song song với một mặt phẳng.
- Điều kiện để ba vectơ đồng phẳng: Cho \(\vec a, \vec b\) là hai vectơ không cùng phương và vectơ \(\vec c\). Ba vectơ \(\vec a, \vec b\) và \(\vec c\) đồng phẳng khi và chỉ khi có hai số thực k, l sao cho: \(\overrightarrow c = k.\overrightarrow a + l.\overrightarrow b .\)
Ví dụ 1:
Cho hình lăng trụ ABC.A’B’C’. Hãy nêu tên các vecto bằng nhau có điểm đầu và điểm cuối là các đỉnh của hình lăng trụ.
Hướng dẫn giải:
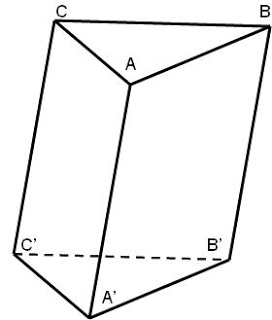
Theo tính chất hình lăng trụ ta có:
\(\begin{array}{l} \overrightarrow {AB} = \overrightarrow {A'B'} ;\,\,\overrightarrow {BC} = \overrightarrow {B'C'} ;\,\,\overrightarrow {CA} = \overrightarrow {C'A'} \\ \overrightarrow {AB} = - \overrightarrow {BA} ;\,\,\overrightarrow {BC} = - \overrightarrow {CB} ;\,\,\overrightarrow {CA} = - \overrightarrow {AC} \\ \overrightarrow {{\rm{AA'}}} = \overrightarrow {BB'} = \overrightarrow {CC'} = - \overrightarrow {{\rm{A'A}}} = - \overrightarrow {B'B} = - \overrightarrow {C'C} . \end{array}\)
Ví dụ 2:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Chứng minh rằng: \(\overrightarrow {SA} + \overrightarrow {SC} = \overrightarrow {SB} + \overrightarrow {SD}\).
Hướng dẫn giải:
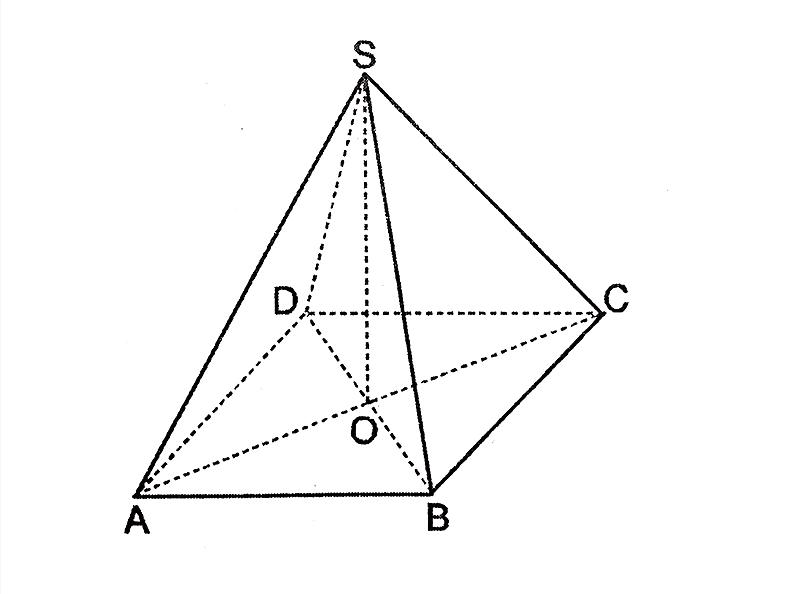
Gọi O là tâm của hình bình hành ABCD. Ta có:
\(\begin{array}{l} \overrightarrow {SA} + \overrightarrow {AO} = \overrightarrow {SO} \\ \overrightarrow {SC} + \overrightarrow {CO} = \overrightarrow {SO} \\ \Rightarrow \overrightarrow {SA} + \overrightarrow {SC} = 2\overrightarrow {SO} (1) \end{array}\)
Theo quy tắc hình bình hành: \(\overrightarrow {{\rm{SB}}} + \overrightarrow {SD} = 2\overrightarrow {SO} (2)\)
Từ (1) và (2) ta có: \(\overrightarrow {SA} + \overrightarrow {SC} = \overrightarrow {SB} + \overrightarrow {SD}\).
Ví dụ 3:
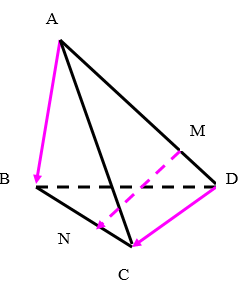
Cho tứ diện ABCD. Trên cạnh AD lấy điểm M sao cho \(\overrightarrow {AM} = 3\overrightarrow {MD}\) và trên cạnh BC lấy điểm N sao cho \(\overrightarrow {NB} = - 3\overrightarrow {NC}\). Chứng tỏ rằng \(\overrightarrow {AB} ,\overrightarrow {DC} ,\overrightarrow {MN}\) đồng phẳng.
Hướng dẫn giải:
Theo giả thiết ta có: \(\overrightarrow {AM} = 3\overrightarrow {MD} \Rightarrow \overrightarrow {MA} = - \overrightarrow {MD}\) và \(\overrightarrow {{\rm{NB}}} = - 3\overrightarrow {NC}\)
Mà: \(\overrightarrow {{\rm{MN}}} = \overrightarrow {MA} + \overrightarrow {AB} + \overrightarrow {BN}\)
và \(\overrightarrow {{\rm{MN}}} = \overrightarrow {MD} + \overrightarrow {DC} + \overrightarrow {CN} (1)\)
\(\Rightarrow 3\overrightarrow {MN} = 3\overrightarrow {MD} + 3\overrightarrow {DC} + 3\overrightarrow {CN} (2)\)
\(\begin{array}{l} (1) + (2) \Rightarrow 4\overrightarrow {MN} = \overrightarrow {MA} + 3\overrightarrow {MD} + \overrightarrow {AB} + 3\overrightarrow {DC} + \overrightarrow {BN} + 3\overrightarrow {CN} \\ \Leftrightarrow 4\overrightarrow {MN} = \overrightarrow {MA} + 3\overrightarrow {MD} \Leftrightarrow \overrightarrow {MN} = \frac{1}{4}\overrightarrow {MA} + \frac{3}{4}\overrightarrow {MD} \end{array}\)
Hệ thức trên chứng tỏ: \(\overrightarrow {AB} ,\overrightarrow {DC} ,\overrightarrow {MN}\) đồng phẳng.
3. Luyện tập Bài 1 chương 3 hình học 11
Nội dung bài học sẽ giúp các em nắm được các khái niệm Vectơ trong không gian, phương pháp chứng minh ba vectơ đồng phẳng. Bên cạnh đó là các ví dụ minh họa sẽ giúp các em hình thành các kĩ năng giải bài tập liên quan đến vectơ trong không gian.
3.1 Trắc nghiệm về Vectơ trong không gian
Để cũng cố bài học xin mời các em cũng làm Bài kiểm tra Trắc nghiệm Hình học 11 Bài 1 để kiểm tra xem mình đã nắm được nội dung bài học hay chưa.
-
- A. \(SA \bot BC\)
- B. \(AH \bot BC\)
- C. \(AH \bot AC\)
- D. \(AH \bot SC\)
-
- A. Mặt phẳng trung trực của đoạn thẳng AB.
- B. Đường trung trực của đoạn thẳng AB .
- C. Mặt phẳng vuông góc với AB tại A .
- D. Đường thẳng qua A và vuông góc với AB .
-
- A. \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 \)
- B. \(\overrightarrow {OA} + \overrightarrow {OC} = \overrightarrow {OB} + \overrightarrow {OD} \)
- C. \(\overrightarrow {OA} + \frac{1}{2}\overrightarrow {OB} = \overrightarrow {OC} + \frac{1}{2}\overrightarrow {OD} \)
- D. \(\overrightarrow {OA} + \frac{1}{2}\overrightarrow {OC} = \overrightarrow {OB} + \frac{1}{2}\overrightarrow {OD} \)
-
- A. \(\overrightarrow a + \overrightarrow c = \overrightarrow b + \overrightarrow d \)
- B. \(\overrightarrow a + \overrightarrow b = \overrightarrow c + \overrightarrow d \)
- C. \(\overrightarrow a + \overrightarrow d = \overrightarrow b + \overrightarrow c \)
- D. \(\overrightarrow a + \overrightarrow b + \overrightarrow c + \overrightarrow d = \overrightarrow 0 \)
Câu 2- Câu 5: Xem thêm phần trắc nghiệm để làm thử Online
3.2 Bài tập SGK và Nâng Cao về Vectơ trong không gian
Bên cạnh đó các em có thể xem phần hướng dẫn Giải bài tập Hình học 11 Bài 1 sẽ giúp các em nắm được các phương pháp giải bài tập từ SGK hình học 11 Cơ bản và Nâng cao.
Bài tập 3.2 trang 129 SBT Hình học 11
Bài tập 3.3 trang 129 SBT Hình học 11
Bài tập 3.4 trang 130 SBT Hình học 11
Bài tập 3.5 trang 130 SBT Hình học 11
Bài tập 3.6 trang 130 SBT Hình học 11
Bài tập 3.7 trang 130 SBT Hình học 11
Bài tập 1 trang 91 SGK Hình học 11 NC
Bài tập 2 trang 91 SGK Toán 11 NC
Bài tập 3 trang 91 SGK Hình học 11 NC
Bài tập 4 trang 91 SGK Hình học 11 NC
Bài tập 5 trang 91 SGK Hình học 11 NC
Bài tập 6 trang 91 SGK Hình học 11 NC
4. Hỏi đáp về bài 1 chương 3 hình học 11
Nếu có thắc mắc cần giải đáp các em có thể để lại câu hỏi trong phần Hỏi đáp, cộng đồng Toán HOCTAP247 sẽ sớm trả lời cho các em.
Copyright © 2021 HOCTAP247

.PNG)
.PNG)
.PNG)