Hình học 11 Bài 3: Đường thẳng vuông góc với mặt phẳng

Đường thẳng a được gọi là vuông góc với mặt phẳng (P) nếu a vuông góc với mọi đường thẳng a nằm trong mặt phẳng (P). 

Kí hiệu: \(a \bot \left ( P \right )\)

Định nghĩa đường thẳng vuông góc mặt phẳng

\(a \bot mp(P) \Leftrightarrow a \bot c,\forall c \subset (P)\)

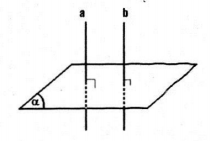
Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b của mặt phẳng (P) thì \(d \bot \left ( P \right ).\)

Hệ quả: Nếu một đường thẳng vuông góc với hai cạnh của một tam giác thì nó cũng vuông góc với cạnh thứ ba của tam giác đó.

Tính chất 1: Có một và chỉ một đường mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.

Tính chất 2: Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.

a) Tính chất 1

• Cho hai đường thẳng song song. Mặt phẳng nào vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng kia.

\(\left. \begin{array}{l} a//b\\ \left( \alpha \right) \bot a \end{array} \right\} \Rightarrow \left( \alpha \right) \bot b\)

• Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.

\(\left. \begin{array}{l} a \bot (\alpha )\\ b \bot (\alpha )\\ a \ne b \end{array} \right\} \Rightarrow a//b\)

b) Tính chất 2

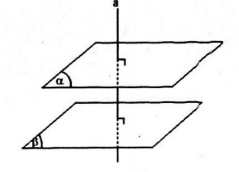
• Cho hai mặt phẳng song song. Đường thẳng nào vuông góc với mặt phẳng này thì cũng vuông góc với mặt phẳng kia.

\(\left. \begin{array}{l} a \bot (\alpha )\\ \left( \alpha \right)//\left( \beta \right) \end{array} \right\} \Rightarrow \left( \alpha \right) \bot \left( \beta \right)\)

• Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.

 

\(\left. \begin{array}{l} a \bot (\alpha )\\ a \bot \left( \beta \right)\\ \left( \alpha \right) \ne \left( \beta \right) \end{array} \right\} \Rightarrow \left( \alpha \right)//\left( \beta \right)\)

c) Tính chất 3

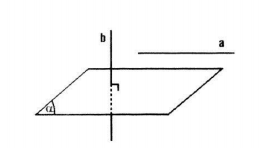
• Cho đường thẳng a và mặt phẳng \(\left ( \alpha \right )\) song song với nhau. Đường thẳng nào vuông góc với \(\left ( \alpha \right )\) thì cũng vuông góc với a.

\(\left. \begin{array}{l} a//(\alpha )\\ b \bot \left( \alpha \right) \end{array} \right\} \Rightarrow b \bot a\)

• Nếu một đường thẳng và một mặt phẳng cùng vuông góc với một đường thẳng khác thì chúng song song với nhau.

\(\left. \begin{array}{l} a \bot b\\ b \bot \left( \alpha \right)\\ a \not\subset \left( \alpha \right) \end{array} \right\} \Rightarrow a//\left( \alpha \right)\)

Cho đường thẳng d nằm trong mặt phẳng \(\left ( \alpha \right )\) và b là đường thẳng không thuộc \(\left ( \alpha \right )\) đồng thời không vuông góc với \(\left ( \alpha \right )\). Gọi b' là hình chiếu vuông góc của b trên \(\left ( \alpha \right )\). Kho đó a vuông góc với b khi và chỉ khi a vuông góc với b'.

• Góc giữa đường thẳng d không vuông góc với mặt phẳng \(\left ( \alpha \right )\) là góc giữa d và hình chiếu d’ của nó trên mặt phẳng \(\left ( \alpha \right )\).

• Đặc biệt: Nếu d vuông góc với mặt phẳng \(\left ( \alpha \right )\) thì ta nói rằng góc giữa đường thẳng d và mặt phẳng \(\left ( \alpha \right )\) là 90⁰.

Cho hình chóp  S.ABC có đáy ABC là tam giác vuông tại C, \(SA \bot (ABC).\)

a) Chứng minh rằng: \(BC \bot (SAC)\).

b) Gọi E là hình chiếu vuông góc của A trên SC. Chứng minh rằng: \(AE \bot (SBC).\)

c) Gọi (P) là mặt phẳng qua AE và vuông góc với SB, (P) giao với SB tại D. Đường thẳng DE cắt BC tại F. Chứng minh rằng: \(AF \bot (SAB).\)

Lời giải:

a) Ta có: \(BC \bot AC{\rm{ }}(gt){\rm{ (1)}}\)

Mặt khác: \(\left. \begin{array}{l} SA \bot (ABC)\\ BC \subset (ABC) \end{array} \right\} \Rightarrow SA \bot BC\,\,(2)\)

Từ (1) và (2) suy ra: \(BC \bot (SAB).\)

b) Ta có: \(AE \bot SC{\rm{ (3) (gt)}}\)

Theo câu a ta có: \(BC \bot (SAB) \Rightarrow AE \bot BC{\rm{ (4)}}\)

Từ (3) (4) suy ra: \(AE \bot (SBC).\)

c) Ta có mặt phẳng (P) chính là mặt phẳng (ADE).

Từ \(\left. \begin{array}{l} SA \bot (ABC)\\ AF \subset (ABC) \end{array} \right\} \Rightarrow AF \bot SA{\rm{ (5)}}\)

Do \(SB \bot (ADE) \Rightarrow AF \bot SB{\rm{ (6)}}\).

Từ (5) (6) suy ra: \(AF \bot (SAB).\)

Ví dụ 2:

Cho hình chóp S.ABCD đáy ABCD là hình thang vuông tại A và B, \(SA \bot (ABCD)\), AD=2a, AB=BC=a. Chứng minh rằng: Tam giác SCD vuông.

Lời giải:

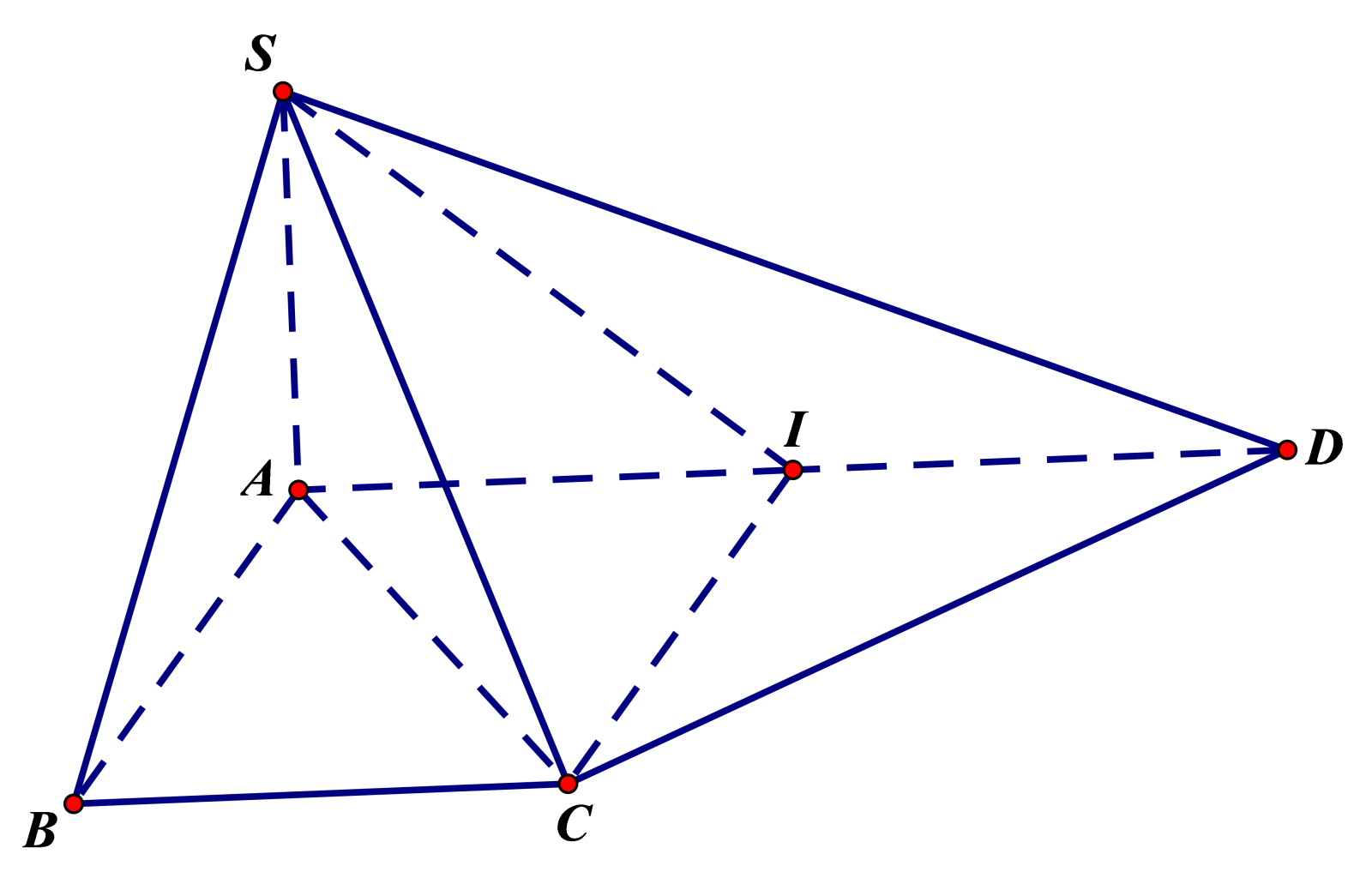
Ta có: \(\left. \begin{array}{l} SA \bot (ABCD)\\ CD \subset (ABCD) \end{array} \right\} \Rightarrow SA \bot CD(1)\)

Gọi I là trung điểm của AD. Tứ giác ABCI là hình vuông.

Do đó, \(\widehat {ACI} = {45^0}.\) (*)

Mặt khác tam giác CID vuông cân tại I nên \(\widehat {BCI} = {45^0}.\) (**)

Từ (*) (**) suy ra: \(\widehat {ACD} = {90^0}\) hay \(AC \bot CD (2)\).

Từ (1) và (2) suy ra: \(CD \bot (SAC) \Rightarrow CD \bot SC\).

Hay tam giác SCD vuông tại C.

Ví dụ 3:

Cho hình chóp S.ABCD đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy, \(SA = a\sqrt 6\). Tính sin của góc giữa:

a) SC và (SAB).

b) AC và (SBC).

Lời giải:

a) Ta có: \(BC \bot AB{\rm{ (gt)}}\).

\(SA \bot BC\) (Vì \(SA \bot (ABCD)\))

Suy ra: \(BC \bot (SAB).\)

Do đó: SB là hình chiếu vuông góc của SC trên mặt phẳng (SAB).

\(\Rightarrow (SC,(SAB)) = \widehat {BSC}.\)

Ta có: \(\sin (SC,(SAB)) = \sin \widehat {BSC} = \frac{{BC}}{{SC}} = \frac{a}{{\sqrt {S{A^2} + A{C^2}} }} = \frac{{\sqrt 2 }}{4}\).

b) Trong  mặt phẳng (SAB) kẻ: \(AH \bot SB{\rm{ (H}} \in {\rm{SB)}}.\)

Theo câu a ta có: \(BC \bot (SAB) \Rightarrow AH \bot BC\) nên \(AH \bot (SBC)\) hay CH là hình chiếu vuông góc của AC trên mặt phẳng (SBC).

\(\Rightarrow (AC,(SBC)) = \widehat {ACH}.\)

Xét tam giác vuông SAB có: \(\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{S{A^2}}} = \frac{7}{{6{a^2}}} \Rightarrow AH = a.\sqrt {\frac{6}{7}} .\)

Vậy: \(\sin (AC,(SBC)) = \sin \widehat {ACH} = \frac{{AH}}{{AC}} = \frac{{\sqrt {21} }}{7}.\) 

Nội dung bài học sẽ giúp các em nắm được khái niệm, cách xác định góc giữa đường thẳng và mặt phẳng, các tính chất, định lý liên quan đến đường thẳng vuông góc với mặt phẳng, mối liên hệ giữa quan hệ song song và quan hệ vuông góc giữa đường thẳng và mặt phẳng. Bên cạnh đó là các ví dụ minh họa sẽ giúp các em hình thành các kĩ năng giải bài tập liên quan đến xác định góc giữa đường thẳng và mặt phẳng, chứng minh đường thẳng vuông góc với mặt phẳng,...

Để cũng cố bài học xin mời các em cũng làm Bài kiểm tra Trắc nghiệm Hình học 11 Bài 3 để kiểm tra xem mình đã nắm được nội dung bài học hay chưa.

• Câu 1:

  Khẳng định nào sau đây sai?

  • A. Nếu đường thẳng \(d \bot \left( \alpha \right)\) thì d vuông góc với hai đường thẳng trong \((\alpha)\)
     
  • B. Nếu đường thẳng d vuông góc với hai đường thẳng nằm trong \((\alpha)\) thì \(d \bot \left( \alpha \right)\)
  • C. Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau nằm trong \((\alpha)\) thì d vuông góc với bất kì đường thẳng nào nằm trong \((\alpha)\)
  • D. Nếu \(d \bot \left( \alpha \right)\) và đường thẳng a || \((\alpha)\) thì \(d\bot a\)

• Câu 2:

  Trong không gian cho đường thẳng \(\Delta\) và điểm O. Qua O có mấy đường thẳng vuông góc với \(\Delta\) cho trước

  • A. 1
  • B. 2
  • C. 3
  • D. Vô số

• Câu 3:

  Qua điểm O cho trước, có bao nhiêu mặt phẳng vuông góc với đường thẳng d cho trước

  • A. 1
  • B. 2
  • C. 3
  • D. vô số

• Câu 4:

  Mệnh đề nào sau đây sai

  • A. Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song
  • B. Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song
  • C. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì song song.
  • D. Một đường thẳng và một mặt phẳng (không chứa đường thẳng đã cho) cùng vuông góc với một đường thẳng thì song song nhau.

• Câu 5:

  Cho hình chóp S.ABC có SA = SB = SC. O là hình chiếu của S lên mặt đáy ABC. Khẳng định nào sau đây đúng?

  • A. O là trọng tâm tam giác ABC
  • B. O là tâm đường tròn ngoại tiếp tam giác ABC
  • C. O là trực tâm tam giác ABC
  • D. O là tâm đường tròn nội tiếp tam giác ABC

Câu 2- Câu 5: Xem thêm phần trắc nghiệm để làm thử Online 

Bên cạnh đó các em có thể xem phần hướng dẫn Giải bài tập Hình học 11 Bài 3 sẽ giúp các em nắm được các phương pháp giải bài tập từ SGK hình học 11 Cơ bản và Nâng cao.

Bài tập 3.19 trang 145 SBT Hình học 11

Bài tập 3.20 trang 145 SBT Hình học 11

Bài tập 3.21 trang 145 SBT Hình học 11

Bài tập 12 trang 102 SGK Hình học 11 NC

Bài tập 13 trang 102 SGK Hình học 11 NC

Bài tập 14 trang 102 SGK Hình học 11 NC

Bài tập 15 trang 102 SGK Hình học 11 NC

Bài tập 16 trang 103 SGK Hình học 11 NC

Bài tập 17 trang 103 SGK Hình học 11 NC

Bài tập 18 trang 103 SGK Hình học 11 NC

Bài tập 19 trang 103 SGK Hình học 11 NC

Bài tập 20 trang 103 SGK Hình học 11 NC

Nếu có thắc mắc cần giải đáp các em có thể để lại câu hỏi trong phần Hỏi đáp, cộng đồng Toán HOCTAP247 sẽ sớm trả lời cho các em.