Trắc nghiệm Vật lý 10 Bài 9 Tổng hợp và phân tích lực và Điều kiện cân bằng của chất...
Câu 1 : Gọi F1 , F2 là độ lớn của hai lực thành phần, F là độ lớn hợp lực của chúng. Câu nào sau đây là đúng ?
A. F không bao giờ nhỏ hơn cả F1 và F2
B. F không bao giờ bằng F1 hoặc F2
C. F luôn luôn lớn hơn cả F1 v F2
D. Trong mọi trường hợp : \(\left| {{F_1} - {F_2}} \right| \le F \le \left| {{F_1} + {F_2}} \right|\)
Câu 2 : Độ lớn của hợp lực hai lực đồng qui hợp với nhau góc \(\alpha \) là :
A. \(F_{}^2 = {F_1}^2 + F_2^2 + 2{F_1}{F_2}\cos \alpha \)
B. \(F_{}^2 = {F_1}^2 + F_2^2 - 2{F_1}{F_2}\)cos\(\alpha \)
C. \(F = {F_1} + F_2^{} + 2{F_1}{F_2}\)
D. \(F_{}^2 = {F_1}^2 + F_2^2 - 2{F_1}{F_2}\)cos\(\alpha \)
Câu 3 : Cho hai lực đồng quy có độ lớn bằng 9 N và 12 N. Trong số các giá trị sau đây, giá trị nào là độ lớn của hợp lực ?
A. 1N
B. 2N
C. 15N
D. 25N
Câu 4 : Cho hai lực đồng quy có cùng độ lớn 10 N. Góc giữa hai lực bằng bao nhiêu thì hợp lực cũng có độ lớn bằng 10 N?
A. 900
B. 1200
C. 600
D. 00
Câu 5 :
Phân tích lực 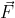 thành hai lực
thành hai lực 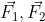 theo hai phương OA và OB (hình vẽ). Giá trị nào sau đây là độ lớn của hai lực thành phần.
theo hai phương OA và OB (hình vẽ). Giá trị nào sau đây là độ lớn của hai lực thành phần.
A. \(F_1 = F_2 = F\)
B. \(F_1 = F_2 =\frac{1}{2}F\)
C. \(F_1 = F_2 = 1,15F\)
D. \(F_1 = F_2 = 0,58F\)
Câu 6 : Khi nói về phép phân tích lực, phát biểu nào sau đây sai?
A. Phân tích lực là thay thế một lực bằng hai hay nhiều lực có tác dụng giống hệt như lực đó.
B. Khi phân tích một lực thành hai lực thành phần thì phải tuân theo quy tắc hình bình hành.
C. Khi phân tích một lực thành hai lực thành phần thì hai lực thành phần làm thành hai cạnh của hình bình hành.
D. Phân tích lực là phép thay thế các lực tác dụng đồng thời vào vật bằng một lực như các lực đó.
Câu 7 : Một chất điểm chịu tác dụng đồng thời của hai lực thành phần vuông góc với nhau có độ lớn lần lượt là F1 = 5 N và F2. Biết hợp lực trên có độ lớn là 25 N. Giá trị của F2 là
A. 10 N.
B. 20 N.
C. 30 N.
D. 40 N.
Câu 8 : Hai lực có giá đồng quy có độ lớn là 3 N là 4 N và có phương vuông góc với nhau. Hợp lực của hai lực nàu có độ lớn là
A. 7 N.
B. 5 N.
C. 1 N.
D. 12 N.
Câu 9 : Một chất điểm chịu tác dụng của hai lực thành phần có độ lớn 6 N là 8 N. Biết hợp lực của hai lực này có giá trị 10 N, góc tạo bởi hai lực này là
A. 90o.
B. 30o.
C. 45o.
D. 60o.
Câu 10 : Hai lực có giá đồng quy có độ lớn 7 N và 13 N. Độ lớn hợp lực của hai lực này không thể có giá trị nào sau đây?
A. 7 N.
B. 13 N.
C. 20 N.
D. 22 N.
Câu 11 : Một vật chịu tác dụng của bốn lực đồng phẳng, đồng quy nằm ngang gồm lực F1 = 10 N hướng về phía Đông, lực F2 = 20 N hướng về phía Bắc, lực F3 = 22 N hướng về phía Tây, lực F4 = 36 N hướng về phía Nam. Độ lớn của hợp lực do các lực này tác dụng lên vật là
A. 28 N.
B. 20 N.
C. 4 N.
D. 26,4 N.
Câu 12 : Hợp lực của hai lực có độ lớn F và 2F có thể
A. nhỏ hơn F.
B. lớn hơn 3F.
C. vuông góc với lực F.
D. vuông góc với lực 2F.
Câu 13 : Lực 10 N là hợp lực của cặp lực nào dưới đây ? Cho biết góc giữa cặp lực đó.
A. 3 N, 15 N ; 120o;
B. 3 N, 13 N ; 180o.
C. 3 N, 6 N ; 60o.
D. 3 N, 5 N ; 0o.
Câu 14 : Một chất điểm đứng yên dưới tác dụng của ba lực 6 N, 8 N và 10 N. Hỏi góc giữa hai lực 6 N và 8 N bằng bao nhiêu ?
A. 30o.
B. 60o.
C. 45o.
D. 90o.
Lời giải có ở chi tiết câu hỏi nhé! (click chuột vào câu hỏi).
Copyright © 2021 HOCTAP247
