Một chất điểm dao động điều hòa có vận tốc được mô tả theo đồ thị bên. Phương trình dao động của vật là
Câu hỏi :
Một chất điểm dao động điều hòa có vận tốc được mô tả theo đồ thị bên. Phương trình dao động của vật là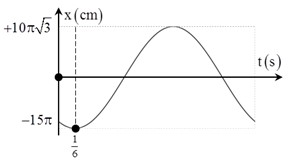
A. \(x=10\sqrt{3}\cos \left( \pi t-\frac{\pi }{3} \right)\,cm.\)
B. \(x=5\sqrt{3}\cos \left( 2\pi t+\frac{\pi }{3} \right)\,cm.\)
C. \(x=5\sqrt{3}\cos \left( 2\pi t-\frac{\pi }{3} \right)\,cm.\)
D. \(x=10\sqrt{3}\cos \left( \pi t+\frac{\pi }{3} \right)\,cm.\)
* Đáp án
D
* Hướng dẫn giải
Đáp án D
+ Từ đồ thị, ta thu được \({{v}_{\max }}=\omega A=10\pi \sqrt{3}\)cm/s.
+ Trong khoảng thời gian \(\Delta t=\frac{1}{6}\text{ }s\) vận tốc của vật giảm từ \(v=-\frac{\sqrt{3}}{2}{{v}_{\max }}\)đến \(-{{v}_{\max }}\)
→ Từ hình vẽ ta có \(\left\{ \begin{array}{l} {\varphi _{0v}} = \frac{{5\pi }}{6}\\ \frac{T}{{12}} = \frac{1}{6} \end{array} \right. \Rightarrow \left\{ \begin{array}{l} {\varphi _{0v}} = \frac{{5\pi }}{6}\\ T = 2 \end{array} \right. \Rightarrow \left\{ \begin{array}{l} \varphi = \pi \\ A = 10\sqrt 3 \end{array} \right.\)
+ Phương trình li độ \(x=10\sqrt{3}\cos \left( \pi t+\frac{\pi }{3} \right)\) cm,
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT QG năm 2022 môn Vật lý - Trường THPT Phạm Văn Đồng
Copyright © 2021 HOCTAP247
