Một vật tham gia đồng thời hai dao động điều hòa cùng phương, cùng tần số, nhưng vuông pha nhau, biên độ tương ứ

* Hướng dẫn giải

Áp dụng phương pháp giản đồ vecto

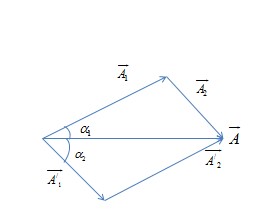
\(\overrightarrow{{{A}_{1}}}\bot \overrightarrow{{{A}_{2}}}\)    (1)

\(\overrightarrow{{{A}_{1}}}\bot \overrightarrow{A_{1}^{/}}\)      (2)

\(\overrightarrow{A}\) không đổi    (3)

Từ (1), (2), (3) ta thấy rằng các điểm \(\overrightarrow{{{A}_{1}}},\overrightarrow{{{A}_{2}}},\overrightarrow{{{A}^{/}}_{1}},\overrightarrow{{{A}^{/}}_{2}},\overrightarrow{A}\) luôn nằm trên đường tròn có đường kính là \(\overrightarrow{A}\). Cho nên tam giác \(\overrightarrow{{{A}_{2}}},\overrightarrow{A},\overrightarrow{A_{2}^{/}}\) vuông tại \(\overrightarrow{A}\)

Vậy, \(A_{2}^{2}+A_{2}^{{{/}^{2}}}={{A}^{2}}\to A_{2}^{2}+{{\left( {{A}_{2}}\sqrt{15} \right)}^{2}}={{16}^{2}}\to {{A}_{2}}=4cm\) → chọn A.