Trang chủ
Đề thi & kiểm tra
Lớp 8
Toán học
Bài tập theo tuần Toán 8 - Tuần 1 !!
Tứ giác ABCD có AB = BC, CD = DA...
Tứ giác ABCD có AB = BC, CD = DA a) Chứng minh rằng BD là đường trung trực của AC
Câu hỏi :
Tứ giác ABCD có AB = BC, CD = DA
a) Chứng minh rằng BD là đường trung trực của AC
b) Cho Tính và
* Đáp án
* Hướng dẫn giải
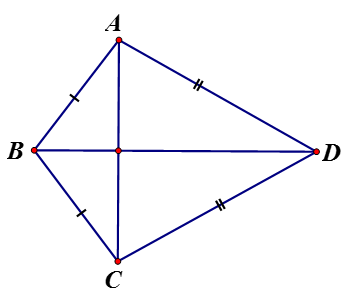
a) Ta có: đường trung trực AC
đường trung trực AC
=> BD là đường trung trực của đoạn thẳng AC.
b) Xét
Tứ giác ABCD có hay
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập theo tuần Toán 8 - Tuần 1 !!
Số câu hỏi: 13
Copyright © 2021 HOCTAP247
