Cho hình thang ABCD (AB//CD) . Gọi P là trung điểm của BC. Đường thẳng đi qua P và song song với cạnh AD cắt đường thẳng AB, CD lần lượt tại Q và R. Biết AD=4cm và khoảng cách từ R...

Câu hỏi :

Cho hình thang ABCD (AB//CD) . Gọi P là trung điểm của BC. Đường thẳng đi qua P và song song với cạnh AD cắt đường thẳng AB, CD lần lượt tại Q và R. Biết AD=4cm và khoảng cách từ R đến AD bằng 3cm . Tính:

$a)S_{AQRD}$

$$\begin{gathered} b\left)S_{ABCD} \\ c\right)S_{hbh}=S_{h.thang} \end{gathered}$$

* Đáp án

* Hướng dẫn giải

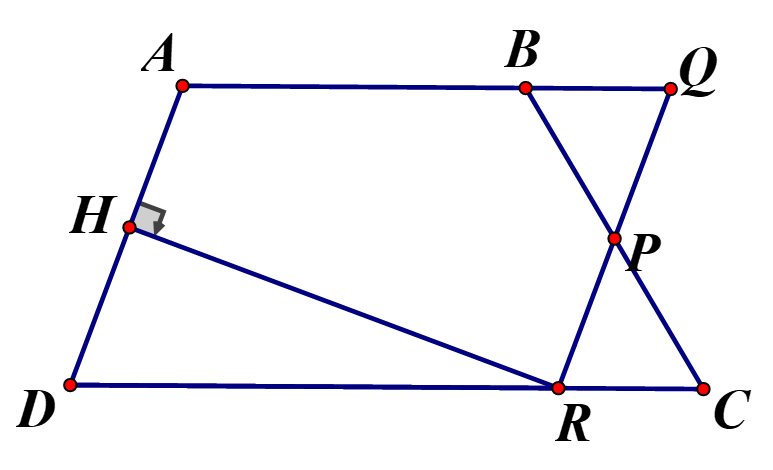
a)     Xét $AQRD$ có :$\left\{\begin{array}{l}AQ//DR\\ AD//QR\end{array}\right.\Rightarrow AQRD$ là hình bình hành

Nên $S_{AQRD}=4.3=12\left(c{m}^2\right)$

b)    Xét $\Delta BPQ$ và $\Delta CPR$ có:

$\widehat{QBP}=\angle RCP$(so le trong), $CP=PB\left(gt\right);\angle CPR=\angle QPB$ (đối đỉnh)

$\Rightarrow S_{ABRD}=S_{ABRPD}+S_{BPQ}=S_{RCP}+S_{ABPRD}=S_{ABCD}$

Vậy $S_{hinhbinhhanh}=S_{hinhthang}$