cho tam giác abc trên tia đối của tia ba lấy điểm M, trên tia đối của tia da lấy điểm N sao cho bm=nd=bd, md cắt bn tại I

* Hướng dẫn giải

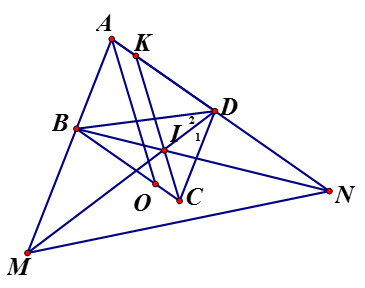
a) $\Delta BMD$ cân do $BM=BD\Rightarrow \widehat{M}=\widehat{D_2}$ mà $\widehat{M}=\widehat{D_1}$ (so le trong) nên $\widehat{D_1}=\widehat{D_2}\Rightarrow ID$ là tia phân giác $\widehat{BDC}$

Chứng minh tương tự BI là phân giác $\widehat{CBD}\Rightarrow I$ là giao điểm 3 đường phân giác

$\Rightarrow CI$ là phân giác $\widehat{BCD}.$Vẽ phân giác Ax của $\widehat{A}$

$\Rightarrow \widehat{xAD}=\widehat{BCK}$ (do $ADCB$ là hình bình hành $\Rightarrow \widehat{A}=\widehat{C})\Rightarrow AK=CO\Rightarrow AKCO$ là hình bình hành $\Rightarrow CI//AO$

b) $\Delta DKC$ cân do $\widehat{KCD}=\widehat{CKD}\Rightarrow CD=CK$ mà $CD=AB\Rightarrow AB=CK$