Trang chủ
Đề thi & kiểm tra
Lớp 8
Toán học
Bài tập theo Tuần toán 8- Tuần 29 !!
Cho tam giác ABC vuông tại A, có AB=6cm, AC=8cm...
Cho tam giác ABC vuông tại A, có AB=6cm, AC=8cm kẻ đường cao AH cắt tia phân giác BD tại K (H thuộc BC, D thuộc AC)
Câu hỏi :
Cho tam giác ABC vuông tại A, có kẻ đường cao AH cắt tia phân giác BD tại K
a) Chứng minh . Tính AH
b) Chứng minh , suy ra hệ thức
Chứng minh cân
Cho tam giác ABC vuông tại A, có kẻ đường cao AH cắt tia phân giác BD tại K
a) Chứng minh . Tính AH
b) Chứng minh , suy ra hệ thức
Chứng minh cân* Đáp án
* Hướng dẫn giải
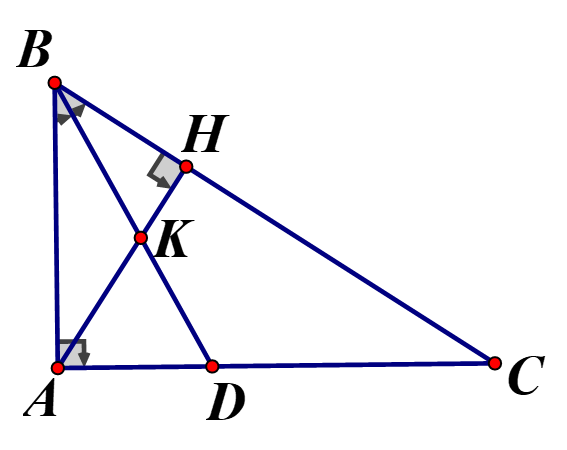
a) Xét và có: chung
b) Xét và có:
(vì BD phân giác)
c) Ta có: (phụ nhau)
(phụ nhau)
Mà là phân giác) và (đối đỉnh)
Nên cân tại A.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập theo Tuần toán 8- Tuần 29 !!
Số câu hỏi: 24
Copyright © 2021 HOCTAP247
