Một đĩa tròn phẳng, mỏng, đồng chất, bán kính R sẽ có điểm đặt của trọng lực tại tâm của đĩa. Hỏi khi khoét một lỗ tròn bán kính [ frac{R}{2} ] (hình 2.19) thì trọng tâm của đĩa sẽ...
Câu hỏi :
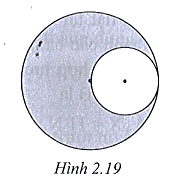
Một đĩa tròn phẳng, mỏng, đồng chất, bán kính R sẽ có điểm đặt của trọng lực tại tâm của đĩa. Hỏi khi khoét một lỗ tròn bán kính \[\frac{R}{2}\] (hình 2.19) thì trọng tâm của đĩa sẽ ở vị trí nào?

* Đáp án
* Hướng dẫn giải
Lời giải
Trọng tâm của đĩa bị khoét là điểm đặt hợp lực của trọng lực PK của hình tròn tâm K bán kính \[\frac{R}{2}\] và trọng lực PI của phần đĩa còn lại sau khi khoét đi hai lỗ tròn đối xứng qua I.
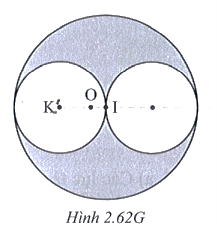
Ta có: \[IK = OK + OI = \frac{R}{2}\]
Vì đĩa phẳng đồng chất nên trọng lượng mỗi phần đĩa tỉ lệ với diện tích. Gọi P là trọng lượng của đĩa nguyên, ta có:
\[\frac{{{P_K}}}{P} = \frac{{\pi {{\left( {\frac{R}{2}} \right)}^2}}}{{\pi {R^2}}} = \frac{1}{4}\]\[ \Rightarrow {P_K} = \frac{P}{4};{P_I} = P - 2{P_K} = \frac{P}{2}\]
Áp dụng quy tắc hợp lực song song cùng chiều cho các trọng lực PI và PK, ta xác định được điểm đặt O của hợp lực sẽ chia đoạn thẳng IK theo tỉ lệ:
\[\frac{{OI}}{{OK}} = \frac{{{P_K}}}{{{P_I}}} = \frac{{\frac{P}{4}}}{{\frac{P}{2}}} = \frac{1}{2} \Rightarrow OI = \frac{R}{6}\]
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải SBT Lí 10 Bài 11: Mô men lực. Điều kiện cân bằng của vật có đáp án !!
Copyright © 2021 HOCTAP247
