cho tam giác ABC vuông tại A (AB > AC) M là trung điểm của AB, P là điểm nằm trong tam giác ABC sao cho MP vuông AB

* Hướng dẫn giải

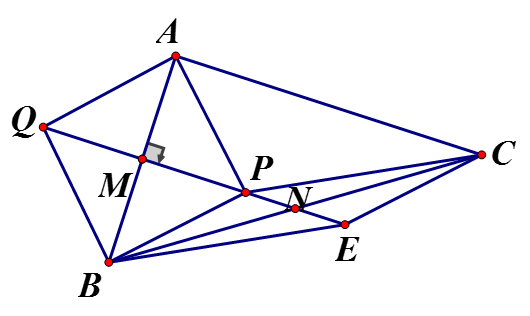
a) Tứ giác AQBP có $\mathrm{QP}\perp \mathrm{AB},\mathrm{AM}=\mathrm{MB},\mathrm{QM}=\mathrm{MP}\Rightarrow \mathrm{AQBP}$ là hình thoi

b) Ta có: $\mathrm{AQ}//\mathrm{EC}$ (cùng $//\mathrm{BP}\mathrm{do}\mathrm{AQBP}$ là hình thoi) và $\mathrm{QE}//\mathrm{AC}$ (cùng $\perp \mathrm{AB})$

$\Rightarrow \mathrm{QACE}$ là hình bình hành

c) Vì AQBP là hình thoi nên $\mathrm{MP}=\frac{1}{2}\mathrm{PQ}\left(1\right)$

Ta có: $\mathrm{BP}//\mathrm{EC}\left(\mathrm{gt}\right);\mathrm{BP}=\mathrm{EC}(=\mathrm{QA})\Rightarrow \mathrm{BPCE}$ là hình bình hành nên PE cắt BC tại trung điểm N mỗi đường nên $\mathrm{NP}=\frac{1}{2}\mathrm{PE}\left(2\right)$

Cộng (1) và (2) vế theo vế ta có: $\mathrm{MP}+\mathrm{NP}=\frac{1}{2}\left(\mathrm{PQ}+\mathrm{PE}\right)\Rightarrow \mathrm{MN}=\frac{1}{2}\mathrm{QE}$

Mà QE = AC (tính chất hình bình hành) nên AC = 2MN

d) $\mathrm{AN}=5\mathrm{cm}\Rightarrow \mathrm{BC}=10\mathrm{cm}$ (Do N là trung điểm BC và AN là đường trung tuyến ứng với cạnh huyền)

$\mathrm{MN}=3\mathrm{cm}\Rightarrow \mathrm{AC}=6\mathrm{cm}\Rightarrow \mathrm{AB}=\sqrt{{\mathrm{BC}}^2-{\mathrm{AC}}^2}=\sqrt{{10}^2-6^2}=8\mathrm{cm}($Áp dụng Pytago)

Nên chu vi $\mathrm{\Delta ABC}:\mathrm{AB}+\mathrm{AC}+\mathrm{BC}=8+6+10=24\left(\mathrm{cm}\right)$