Cho tam giác ABC là trung điểm của BC. Gọi A' là điểm đối xứng của A qua O a) Tứ giác ABA'C là hình gì ? Vì sao ?

Câu hỏi :

Cho $\mathrm{\Delta ABC},\mathrm{O}$ là trung điểm của BC. Gọi A' là điểm đối xứng của A qua O

a) Tứ giác ABA'C là hình gì ? Vì sao ?

b) Để tứ giác ABA'C là hình vuông thì $\mathrm{\Delta ABC}$ cần có điều kiện gì ?

c) Gọi M, N lần lượt là trung điểm của A'B và AC. Chứng minh M, O, N thẳng hàng

* Đáp án

* Hướng dẫn giải

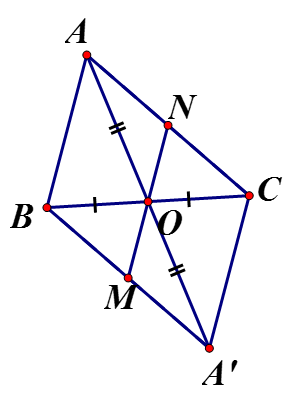
a) Tứ giác ACA'B có: hai đường chéo AA' và BC cắt nhau tại trung điểm O mỗi đường

Nên ACA'B là hình bình hành

b) Hình bình hành ACA'B là hình chữ nhật $\iff \left\{\begin{array}{l}\mathrm{AB}=\mathrm{AC}\\ \mathrm{AB}\perp \mathrm{AC}\end{array}\right.\Rightarrow \mathrm{\Delta ABC}$ vuông cân thì ACA'B là hình vuông

c) $\mathrm{\Delta AA}\text{'}\mathrm{B}$ có D là trung điểm AA', M là trung điểm A'B => OM là đường trung bình $\mathrm{\Delta AA}\text{'}\mathrm{B}\Rightarrow \mathrm{OM}//\mathrm{AB},$ Chứngminh tương tự => ON // AC mà AB // AC nên từ O vẽ được 2 đoạn thẳng OM, ON cùng song song với AB

=> M, O, N thẳng hàng