Cho tứ giác EFGH. Gọi A, B, C, D lần lượt là trung điểm của FH, EF, EG, GH

Câu hỏi :

Cho tứ giác EFGH. Gọi A, B, C, D lần lượt là trung điểm của FH, EF, EG, GH.

a) Chứng minh tứ giác ABCD là hình bình hành

b) Tìm điều kiện của tứ giác EFGH để ABCD là hình thoi (Vẽ hình)

* Đáp án

* Hướng dẫn giải

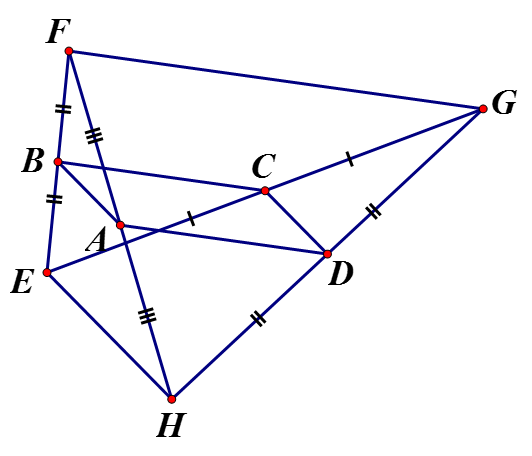
a) Xét $\mathrm{\Delta FGH}$ có: A là trung điểm FH, D là trung điểm HG

$\Rightarrow \mathrm{AD}$ là đường trung bình $\mathrm{\Delta FHG}\Rightarrow \mathrm{AD}=\frac{1}{2}\mathrm{FG},\mathrm{AD}//\mathrm{FG}\left(1\right)$

Xét $\mathrm{\Delta EFG}$ có B là trung điểm EF, C là trung điểm EG nên BC là đường trung bình $\mathrm{\Delta FEG}\Rightarrow \mathrm{BC}=\frac{1}{2}\mathrm{FG},\mathrm{BC}//\mathrm{FG}\left(2\right)$

Từ (1) và (2) suy ra $\mathrm{BC}=\mathrm{AD},\mathrm{BC}//\mathrm{AD}\Rightarrow \mathrm{ABCD}$ là hình bình hành.

b) ABCD là hình thoi $\iff \mathrm{AD}=\mathrm{CD}\left(3\right)$

Chứng minh tương tự câu a => CD là đường trung bình $\mathrm{\Delta EGH}\Rightarrow \mathrm{CD}=\frac{1}{2}\mathrm{EH}\left(4\right)$

Từ (1), (3), (4) $\Rightarrow \mathrm{AD}=\mathrm{CD}\iff \mathrm{FG}=\mathrm{EH}$

Vậy khi tứ giác EFGH có FG = EH thì ABCD là hình thoi.