Cho tam giác ABC trung tuyến AD, gọi E là trung điểm của AB, N là điểm đối xứng của điểm D qua E.

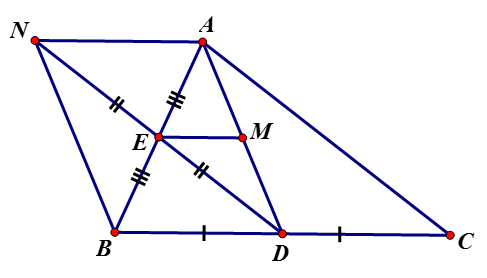
1)Ta có tứ giác ADBN có 2 đường chéo AB và DN cắt nhau tại trung điểm E mỗi đường

Nên ADBN là hình bình hành

2)

a) ADBN là hình chữ nhật khi $\widehat{\mathrm{ADB}}=90°\Rightarrow \mathrm{AD}\perp \mathrm{BC}$. Khi đó $\mathrm{\Delta ABC}$ có AD vừa là đường cao, vừa là trung tuyến nên $\mathrm{\Delta ABC}$ cân tại A.

b) ADBN là hình thoi $\iff \mathrm{AB}\perp \mathrm{DN}$ tại E, khi đó $\mathrm{DE}\perp \mathrm{AB}$ mà DE // AC (tính chất đường trung bình) $\Rightarrow \mathrm{AC}\perp \mathrm{AB}\Rightarrow \mathrm{\Delta ABC}$ vuông tại A thì ADBN là hình thoi.

c) ANBD là hình vuông <=> ANBD vừa là hình thoi, vừa là hình chữ nhật

khi đó $\mathrm{\Delta ABC}$ vuông cân tại A

3) Ta có AN = BD = DC nên AN = DC

Và AN // BD ( do ANBD là hình bình hành) mà $\mathrm{C}\in \mathrm{BD}\Rightarrow \mathrm{AN}//\mathrm{DC}\&\mathrm{AN}=\mathrm{DC}$

Suy ra ANDC là hình bình hành mà $\mathrm{AD}\cap \mathrm{NC}=\mathrm{M}\Rightarrow \mathrm{M}$ là trung điểm AD

$\mathrm{\Delta ABD}$ có E là trung điểm AB, M là trung điểm AD

 => EM là đường trung bình $\mathrm{\Delta ABD}\Rightarrow \mathrm{EM}=\frac{1}{2}\mathrm{BD}$ mà $\mathrm{BD}=\frac{1}{2}\mathrm{BC}$ (D là trung điểm BC)