Trang chủ
Đề thi & kiểm tra
Lớp 8
Toán học
Trắc nghiệm chuyên đề Toán 8 Chủ đề 6. Ôn tập và kiểm tra có đáp án !!
b) Cho ngũ giác đều ABCDE. Gọi F là giao...
b) Cho ngũ giác đều ABCDE. Gọi F là giao điểm hai đường chéo AC và BE.
Câu hỏi :
b) Cho ngũ giác đều ABCDE. Gọi F là giao điểm hai đường chéo AC và BE. Chứng minh tứ giác CFED là hình thoi.
* Đáp án
* Hướng dẫn giải
b) Vì ABCDE là ngũ giác đều nên
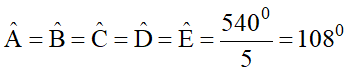
Mặt khác, ΔABC cân tại B nên:
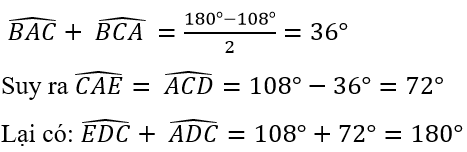
Suy ra ED // AC hay ED // CF.
Chứng minh tương tự ta có EF // CD
Mặt khác ED = DC (gt) nên tứ giác CEFD là hình thoi.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Trắc nghiệm chuyên đề Toán 8 Chủ đề 6. Ôn tập và kiểm tra có đáp án !!
Số câu hỏi: 67
Copyright © 2021 HOCTAP247
