Cho hình bình hành ABCD có diện tích S. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA.

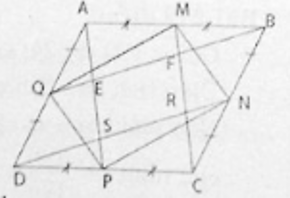
a) Ta có AB // CD (gt)

Suy ra AM // CP    (1)

Lại có AM = AB/2; CP = CD/2    (2)

Từ (1) và (2) suy ra AMCP là hình bình hành

Suy ra AP // CM hay ES // FR.

Tương tự ta cũng chứng minh được tứ giác BQDN là hình bình hành nên BQ // DN. Suy ra EF // RS.

Vậy tứ giác EFRS là hình bình hành