Trang chủ
Đề thi & kiểm tra
Lớp 8
Toán học
Trắc nghiệm chuyên đề Toán 8 Chủ đề 6. Ôn tập và kiểm tra có đáp án !!
Cho hình chữ nhật ABCD. Qua E là một điểm...
Cho hình chữ nhật ABCD. Qua E là một điểm bất kỳ nằm trrên đường chéo AC, kẻ hai đường chéo FG//AD và HK//AB
Câu hỏi :
Cho hình chữ nhật ABCD. Qua E là một điểm bất kỳ nằm trrên đường chéo AC, kẻ hai đường chéo FG//AD và HK//AB ( F ∈ AB, G ∈ DC, H ∈ AD, K ∈ DC ). Chứng minh rằng hai hình chữ nhật EFBK và EGDH có cùng diện tích.
* Đáp án
* Hướng dẫn giải
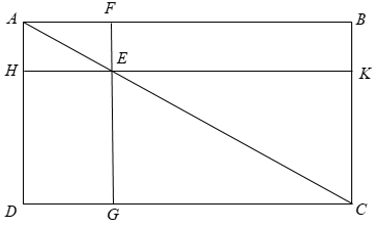
Theo giả thiết ta có FG//AD, HK//AB nên HE//AF và AH//EF.
Xét tứ giác AFEH có:
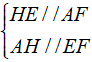
⇒ AFEH là hình bình hành.
Mà Aˆ = 900 ⇒ AFEH là hình chữ nhật.
⇒ Δ AFE = Δ AHE ( c - g - c ) → SAFE = SAHE.
Tương tự: SEKC = SEGC; SABC = SADC
⇒ SABC - SAFE - SEKC = SADC - SAHE - SEGC hay SEFBK = SEHDG.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Trắc nghiệm chuyên đề Toán 8 Chủ đề 6. Ôn tập và kiểm tra có đáp án !!
Số câu hỏi: 67
Copyright © 2021 HOCTAP247
