Trung tuyến AD và BE của Δ ABC cắt nhau tại G. Chứng minh rằng: SDEG = 1/2SCEG = 1/3SCED = 1/4SABG = 1/6SABE = 1/12SABC.

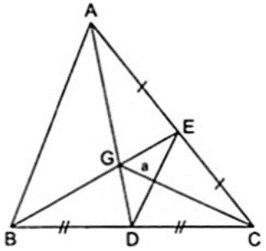
Đặt S_DEG = a. Ta cần chứng minh:

S_CEG = 2a; S_CED = 3a; S_ABG = 4a; S_ABE = 6a; S_ABC = 12a

Đường trung tuyến AD và BE cứt nhau tại G nên G là trọng tâm của Δ ABC

⇒ Khoảng cách từ G đến các đỉnh của tam giác bằng $\frac{2}{3}$ độ dài các đường trung tuyến tương ứng.

Ta có S_BDG = 2S_DGE = 2a (vì chung đường cao kẻ từ D xuống BE và BG = 2GE )

S_BDG = S_CGD = 2a (vì chung đường cao kẻ từ G xuống BC và BD = DC )

Do đó S_BDC = S_BDG + S_CGD = 2a + 2a = 4a.

Lại có S_CEG = $\frac{1}{2}$S_BGC = $\frac{1}{2}$.4a = 2a (vì chung đường cao kẻ từ C xuống BE và BG = 2GE )

+ S_EDC = S_EBD = 2a + a = 3a (vì chung đường cao kẻ từ E xuống BC và BD = DC )

+ S_AGB = 2S_GBD = 4a (vì chung đường cao kẻ từ B xuống AD và AG = 2GD )

+ S_AEB = $\frac{3}{2}$S_AGB = $\frac{3}{2}$.4a = 6a (vì chung đường cao kẻ từ A xuống BE và BE = $\frac{3}{2}$BG )

+ S_ABC = 2S_ABE = 2.6a = 12a.