Trên 3 cạnh AB, BC, CA của Δ ABC lấy ba đoạn AD, BE, CF mỗi đoạn dài bằng 1/3 độ dài

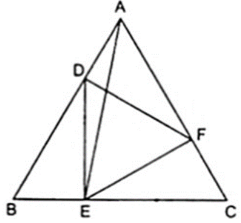
Đặt S_ABC = 9a. Ta có:

+ S_ABE = $\frac{1}{3}$S_ABC = $\frac{1}{3}$.9a = 3a (vì chung đường cao kẻ từ A xuống BC và BC = 3BE)

+ S_ADE = $\frac{1}{3}$S_ABE = $\frac{1}{3}$.3a = a (vì chung đường cao kẻ từ E xuống AB và AB = 3AD )

Do đó S_BDE = S_ABE - S_ADE = 3a - a = 2a.

Tương tự: S_ADF = S_CEF = 2a

Vậy S_DEF = 9a - 6a = 3a hay S_ABC = 3S_DEF.