Trang chủ
Đề thi & kiểm tra
Lớp 8
Toán học
Trắc nghiệm chuyên đề Toán 8 Chủ đề 5: Diện tích xung quanh hình chóp đều. Thể tích của hình chóp đều có đáp án !!
Tính diện tích toàn phần của hình chóp tam giác...
Tính diện tích toàn phần của hình chóp tam giác đều có cạnh đáy bằng a và chiều cao bằng 2a. Hướng dẫn giải
Câu hỏi :
Tính diện tích toàn phần của hình chóp tam giác đều có cạnh đáy bằng a và chiều cao bằng 2a.
* Đáp án
* Hướng dẫn giải
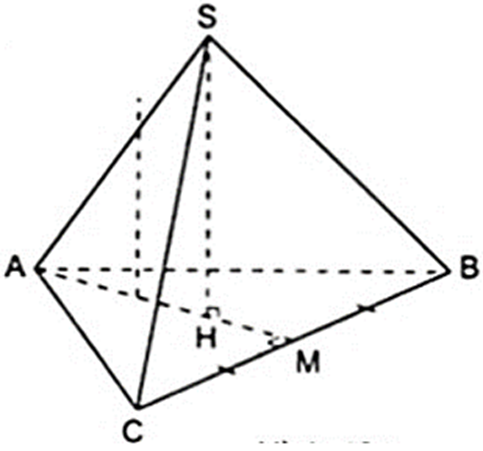
Xét hình chóp S.ABC có AB = AC = BC = a và SH = 2a.
Gọi M là trung điểm của BC thì AM vừa là đường trung tuyến, vừa là đường cao, vừa là đường phân giác của tam giác đều ABC nên AM ⊥ BC và HM = 1/3AM.
Áp dụng định lý Py – ta – go vào tam giác vuông ABM vuông tại M ta được:
AB2 = BM2 + AM2 ⇒ a2 = ( a/2 )2 + AM2
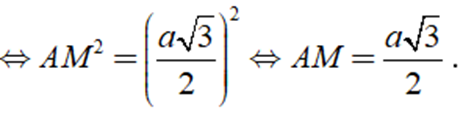
Do đó HM = (a√3) /6.
Áp dụng định lí Py – ta – go vào tam giác vuông SHM vuông tại H, ta có:
SM2 = HM2 + SH2 ⇒ SM2 = ( (a√3) /6 )2 + ( 2a )2
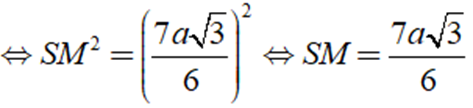
Áp dụng công thức: Stp = Sxq + Sd
Ta có:
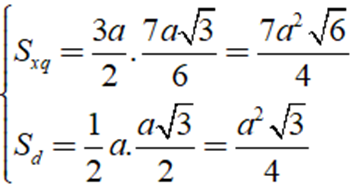
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Trắc nghiệm chuyên đề Toán 8 Chủ đề 5: Diện tích xung quanh hình chóp đều. Thể tích của hình chóp đều có đáp án !!
Số câu hỏi: 8
Copyright © 2021 HOCTAP247
