Cho tam giác ABC vuông tại A (AB < AC).Gọi I là trung điểm của cạnh BC. Qua I vẽ IM vuông góc với AB tại M và IN vuông góc với AC tại N. a) Chứng minh tứ giác AMIN là hình chữ nhật...
Câu hỏi :
Cho tam giác ABC vuông tại A (AB < AC).Gọi I là trung điểm của cạnh BC. Qua I vẽ IM vuông góc với AB tại M và IN vuông góc với AC tại N.
a) Chứng minh tứ giác AMIN là hình chữ nhật.
b) Gọi D là điểm đối xứng của I qua N. Chứng minh tứ giác ACID là hình thoi.
c) Cho AC = 20cm, BC = 25cm.Tính diện tích ΔABC
d) Đường thẳng BN cắt cạnh DC tại K. Chứng minh:
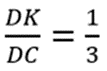
Cho tam giác ABC vuông tại A (AB < AC).Gọi I là trung điểm của cạnh BC. Qua I vẽ IM vuông góc với AB tại M và IN vuông góc với AC tại N.
a) Chứng minh tứ giác AMIN là hình chữ nhật.
b) Gọi D là điểm đối xứng của I qua N. Chứng minh tứ giác ACID là hình thoi.
c) Cho AC = 20cm, BC = 25cm.Tính diện tích ΔABC
d) Đường thẳng BN cắt cạnh DC tại K. Chứng minh:
* Đáp án
* Hướng dẫn giải
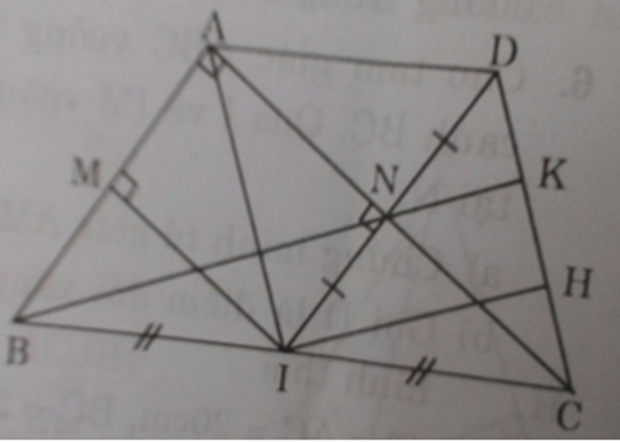
a) Xét tứ giác AMIN có:
∠(MAN) = ∠(ANI) = ∠(IMA) = 90o
⇒ Tứ giác AMIN là hình chữ nhật (có 3 góc vuông).
b) ΔABC vuông có AI là trung tuyến nên AI = IC = BC/2
do đó ΔAIC cân có đường cao IN đồng thời là đường trung tuyến
⇒ NA = NC.
Mặt khác ND = NI (t/c đối xứng) nên ADCI là hình bình hành
Lại có AC ⊥ ID (gt). Do đó ADCI là hình thoi.
c) Ta có: AB2 = BC2 – AC2 (định lí Py-ta-go)
= 252 – 202 ⇒ AB = √225 = 15 (cm)
Vậy SABC = (1/2).AB.AC = (1/2).15.20 = 150 (cm2)
d) Kẻ IH // BK ta có IH là đường trung bình của ΔBKC
⇒ H là trung điểm của CK hay KH = HC (1)
Xét ΔDIH có N là trung điểm của DI, NK // IH (BK // IH)
Do đó K là trung điểm của DH hay DK = KH (2)
Từ (1) và (2) ⇒ DK = KH = HC ⇒ DK/DC= 1/3.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Trắc nghiệm chuyên đề Toán 8 Chủ đề 1: Kiểm tra học kì 1 có đáp án !!
Copyright © 2021 HOCTAP247
