Cho tam giác ABC( AB > AC ) có góc A = 50 độ. Trên cạnh AB lấy điểm D sao cho BD = AC. Gọi E, F lần lượt là

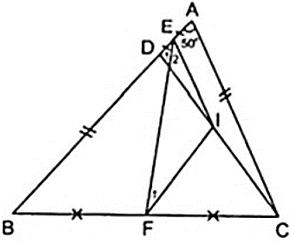
Do E,F lần lượt là trung điểm của cạnh AD,BC theo giả thiết nên ta vẽ thêm I là trung điểm của CD nên EI, FI theo thứ tự lần lượt là đường trung bình của tam giác BCD và ACD.

Đặt BD = AC = 2a

Áp dụng định lý đường trung bình của hai tam giác trên ta có:

( 1 )      FI//BD       ( 2 )       FI = a

( 3 )      EI = a       ( 4 )      EI//AC

Từ ( 1 ) ⇒ $\widehat{E_1}=\widehat{F_1}$ (vì so le trong)       ( 5 )

Từ ( 2 ) và ( 3 ) ⇒ FI = EI nên $\widehat{E_2}=\widehat{F_1}$ (vì trong tam giác, đối diện với hai cạnh bằng nhau là hai góc bằng nhau)       ( 6 )

Từ ( 5 ) và ( 6 ) ⇒ $\widehat{E_1}=\widehat{E_2}$

Từ ( 4 ) ⇒ $\widehat{BEI}=\hat{A}$ = 50⁰ (vì đồng vị)

Mà $\widehat{BEI}=2\widehat{E_1}\Rightarrow \widehat{E_1}$ = 25⁰