Cho hình bình hành ABCD. Gọi E là điểm đối xứng với D qua điểm A, F là điểm đối xứng với D
Câu hỏi :
Cho hình bình hành ABCD. Gọi E là điểm đối xứng với D qua điểm A, F là điểm đối xứng với D qua C. Chứng minh rằng E đối xứng với F qua B.
Cho hình bình hành ABCD. Gọi E là điểm đối xứng với D qua điểm A, F là điểm đối xứng với D qua C. Chứng minh rằng E đối xứng với F qua B.
* Đáp án
* Hướng dẫn giải
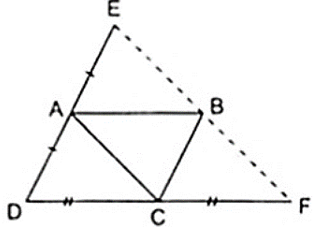
Theo giả thiết ta có:
+ A là trung điểm của DE thì AD = AE ( 1 )
+ C là trung điểm của DF thì CD = CF ( 2 )
Ta có ABCD là hình bình hành nên AD//BC
⇒ AE//BC ( 3 ) và AD = BC ( 4 )
Từ ( 1 ), ( 4 ) ⇒ AE = BC ( 5 )
Từ ( 3 ) và ( 5 ), tứ giác ACBE có cặp cạnh đối song song và bằng nhau nên là hình bình hành.
Áp dụng tính chất và định nghĩa về hình bình hành ACBE ta được
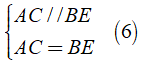
Chứng minh tương tự, tứ giác ACBF là hình bình hành
Ta được:
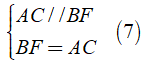
Từ ( 6 ), ( 7 ) ⇒ E, B, F thẳng hàng và BE = BF do đó B là trung điểm của EF hay E đối xứng với F qua B.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Trắc nghiệm chuyên đề Toán 8 Chủ đề 8: Đối xứng tâm có đáp án !!
Copyright © 2021 HOCTAP247
