Cho tam giác ABC, đường cao AH. Gọi I là trung điểm của AC, E là điểm đối xứng với H qua I.

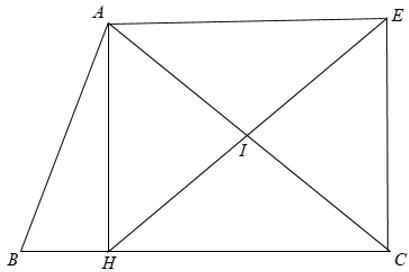
+ Trong Δ AHC vuông có I là trung điểm của AC

⇒ HE là đường trung tuyến của Δ AHC.

⇒ HI = $\frac{1}{2}$AC = AI = IC.

Mà E đối xứng với H qua I ⇒ HI = IE.

Khi đó ta có HI = IE = AI = IC.

+ Xét Δ HCE có CI là đường trung tuyến ứng với cạnh HE

mà CI = $\frac{1}{2}$HE ⇒ Δ HCE vuông tại C.

Tương tự xét với Δ AHE,Δ AEC đều là các tam giác vuông tại A, E.

Xét tứ giác AHCE có $\widehat{EAH}=\widehat{AHC}=\widehat{HCE}=\widehat{CEA}$ = 90⁰