Tứ giác ABCD có hai đường chéo vuông góc với nhau. Gọi E, F, G, H lần lượt là trung điểm của các

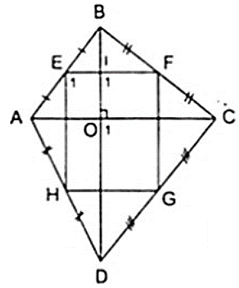
Tứ giác EFGH là hình chữ nhật.

Giải thích: Theo giả thiết ta có EF, GH lần lượt là đường trung bình của tam giác Δ ABC,Δ ADC

Áp dụng định lí đường trung bình vào hai tam giác ta được

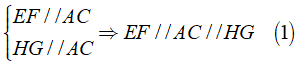
Chứng minh tương tự: EH//FG//BD      ( 2 )

Từ ( 1 ) và ( 2 ), tứ giác EFGH có hai cặp cạnh đối song song nên tứ giác EFGH là hình bình hành.

Gọi O là giao điểm của AC và BD, I là giao điểm của EF với BD.

Áp dụng tính chất của các góc đồng vị vào các đường thẳng song song ở trên và giả thiết nên ta có:

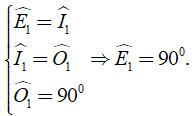
Hình bình hành EFGH có một góc vuông nên EFGH là hình chữ nhật.