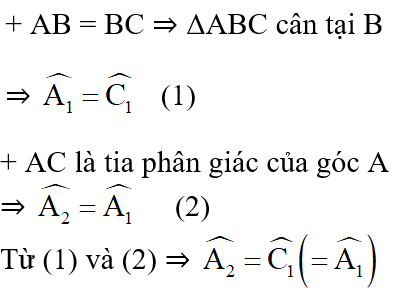Trang chủ
Đề thi & kiểm tra
Lớp 8
Toán học
Giải toán 8: Chương 1: Tứ giác !!
Tứ giác ABCD có AB = BC và AC là...
Tứ giác ABCD có AB = BC và AC là tia phân giác của góc A
Câu hỏi :
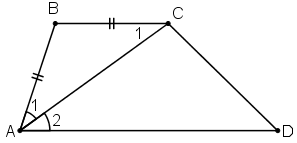
Tứ giác ABCD có AB = BC và AC là tia phân giác của góc A. Chứng minh rằng ABCD là hình thang.
* Đáp án
* Hướng dẫn giải
* Để chứng minh ABCD là hình thang ta cần chứng minh AD // BC.
Thông thường để chứng minh hai đường thẳng song song ta có thể chọn một trong các cách:
+ Chứng minh hai góc so le trong bằng nhau hoặc hai góc đồng vị bằng nhau.
+ Chứng minh hai đường thẳng cùng song song hoặc cùng vuông góc với đường thẳng thứ ba.
Ở bài này ta sẽ đi chứng minh hai góc so le trong bằng nhau là góc A2 và C1.
Theo giả thiết ta có:
Mà hai góc này ở vị trí so le trong
⇒ AD // BC
Vậy ABCD là hình thang (đpcm).
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải toán 8: Chương 1: Tứ giác !!
Số câu hỏi: 134
Copyright © 2021 HOCTAP247