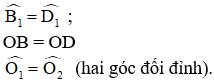Trang chủ
Đề thi & kiểm tra
Lớp 8
Toán học
Giải toán 8: Chương 1: Tứ giác !!
Cho hình bình hành ABCD, O là giao điểm của...
Cho hình bình hành ABCD, O là giao điểm của hai đường chéo
Câu hỏi :
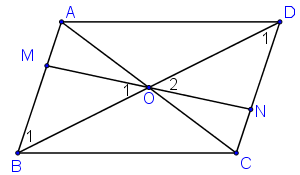
Cho hình bình hành ABCD, O là giao điểm của hai đường chéo. Một đường thẳng đi qua O cắt các cạnh AB và CD theo thứ tự ở M và N. Chứng minh rằng điểm M đối xứng với điểm N qua O.
* Đáp án
* Hướng dẫn giải
+ ABCD là hình bình hành có O là giao điểm hai đường chéo
⇒ OB = OD.
+ ABCD là hình bình hành ⇒ AB // CD ⇒ 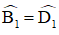
Hai tam giác BOM và DON có:
⇒ ΔBOM = ΔDON (g.c.g)
⇒ OM = ON
⇒ O là trung điểm của MN
⇒ M đối xứng với N qua O.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải toán 8: Chương 1: Tứ giác !!
Số câu hỏi: 134
Copyright © 2021 HOCTAP247