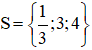Trang chủ
Đề thi & kiểm tra
Lớp 8
Toán học
Giải toán 8: Chương 3: Phương Trình Bậc Nhất Một Ẩn !!
Giải phương trình: (3x – 1)(x^2 + 2) = (3x...
Giải phương trình: (3x – 1)(x^2 + 2) = (3x – 1)(7x – 10).
Câu hỏi :
Giải phương trình: (3x – 1)(x2 + 2) = (3x – 1)(7x – 10).
* Đáp án
* Hướng dẫn giải
(3x – 1)(x2 + 2) = (3x – 1)(7x – 10)
⇔ (3x – 1)(x2 + 2) – (3x – 1)(7x – 10) = 0
⇔ (3x – 1)(x2 + 2 – 7x + 10) = 0
⇔ (3x – 1)(x2 – 7x + 12) = 0
⇔ (3x – 1)(x2 – 4x – 3x + 12) = 0
⇔ (3x – 1)[(x2 – 4x) – (3x - 12)] = 0
⇔ (3x – 1)[x(x – 4) – 3(x – 4)] = 0
⇔ (3x – 1)(x – 3)(x – 4) = 0
⇔ 3x – 1 = 0 hoặc x – 3 = 0 hoặc x – 4 = 0
+ 3x – 1 = 0 ⇔ 3x = 1 ⇔ x = 1/3.
+ x – 3 = 0 ⇔ x = 3.
+ x – 4 = 0 ⇔ x = 4.
Vậy phương trình có tập nghiệm là
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải toán 8: Chương 3: Phương Trình Bậc Nhất Một Ẩn !!
Số câu hỏi: 140
Copyright © 2021 HOCTAP247