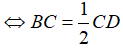Cho hình bình hành ABCD. Các điểm M, N theo thứ tự là trung điểm
Câu hỏi :
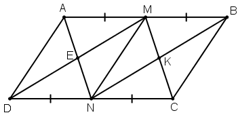
Cho hình bình hành ABCD. Các điểm M, N theo thứ tự là trung điểm của AB, CD. Gọi E là giao điểm của AN và DM, K là giao điểm BN và CM. Hình bình hình ABCD phải có điều kiện gì để tứ giác MENK là:
* Đáp án
* Hướng dẫn giải
ABCD là hình bình hành ⇒ AB = CD.
M là trung điểm AB ⇒ AM = MB = AB/2.
N là trung điểm CD ⇒ CN = DN = CD/2.
⇒ AM = MB = CN = DN.
+ Tứ giác BMDN có: BM // DN và BM = DN
⇒ BMDN là hình bình hành
⇒ DM // BN hay ME // NK
+ Tứ giác AMCN có: AM // NC, AM = NC
⇒ AMCN là hình bình hành
⇒ AN // CM hay EN // MK.
+ Tứ giác MENK có: ME // NK và NE // MK
⇒ MENK là hình bình hành.
a) MENK là hình thoi
⇔ MN ⊥ EK.
⇔ CD ⊥ AD (Vì EK // CD và MN // AD)
⇔ ABCD là hình chữ nhật.
b) MENK là hình chữ nhật
⇔ MN = EK
Mà MN = BC; 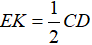
⇔ CD = 2.BC.
c) MENK là hình vuông
⇔ MENK là hình thoi và đồng thời là hình chữ nhật
⇔ ABCD là hình chữ nhật và có CD = 2.BC.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải toán 8: Chương 4: Hình Lăng Trụ Đứng. Hình Chóp Đều !!
Copyright © 2021 HOCTAP247