Một con lắc lò xo dao động điều hòa với phương trình (x = Acos (omega t + frac{5 pi }{6})).

* Hướng dẫn giải

\(x = A\cos (\omega t + \frac{5\pi }{6}) \Rightarrow t = 0: \left\{\begin{matrix} x = -\frac{A\sqrt{3}}{2}\\ v < 0 \ \ \ \ \ \ \end{matrix}\right.\)

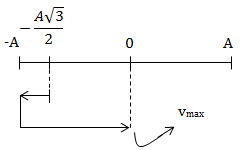
\(\\ t_K = t_1 + kT = \frac{T}{12} + \frac{T}{4} + kT = \frac{T}{3} + kT \\ \Rightarrow t_1 = \frac{T}{3}\ (k=0)\)