Hai dao động điều hòa có cùng phương, cùng tần số có phương trình  và  cm.

* Hướng dẫn giải

\(\begin{matrix} \left\{\begin{matrix} x_1 = A_1\cos (\omega t - \frac{\pi }{6})\\ x_2 = A_2\cos (\omega t - \pi) \end{matrix}\right.\hspace{1,5cm}\\ \Rightarrow x = x_1 + x_2 = 9\cos (\omega t + \varphi ) \end{matrix} \Rightarrow \left\{\begin{matrix} A_{2\ max}\\ A_1 = \ ? \end{matrix}\right.\)

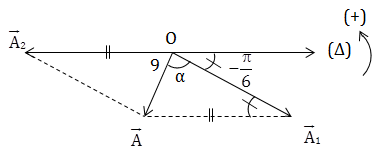
\(+\ \frac{A_2}{\sin \alpha } = \frac{9}{\sin \frac{\pi }{6}} = 18 \Rightarrow A_2 = 18.\sin \alpha\)
\(\Rightarrow \left\{\begin{matrix} A_{2\ max} = 18 \ \ \ \ \ \ \ \ \ \\ \sin \alpha = 1 \Rightarrow \alpha = \frac{\pi }{2} \end{matrix}\right.\)
\(\Rightarrow A_1 = \sqrt{18^2 - 9^2} = 9\sqrt{3}\ cm\)