Hai dao động cùng phương lần lượt có phương trình (x_1 = A_1cos (pi t + frac{pi }{6})) (cm) và (x_2 = 6cos (pi

* Hướng dẫn giải

\(\left\{\begin{matrix} x_1 = A_1\cos(\pi t + \frac{\pi }{6})\\ x_2 = 6\cos(\pi t - \frac{\pi }{2}) \ \ \end{matrix}\right.\)
\(x = x_1 + x_2 = A\cos (\omega t + \varphi )\)


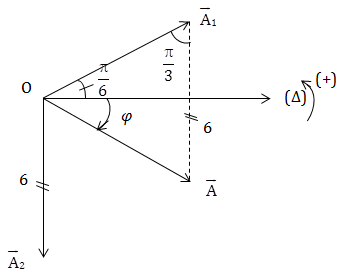
\(\frac{A}{\sin \frac{\pi }{3}} = \frac{6}{\sin \left ( \frac{\pi}{6} + |\varphi |\right )}\)
\(\Rightarrow A = \frac{3\sqrt{3}}{\sin \left ( \frac{\pi }{6} + |\varphi |\right )}\)
\(A_{min} = \sin \left ( \frac{\pi }{6} + |\varphi |\right ) = 1 \Rightarrow |\varphi | = \frac{\pi }{3} \Rightarrow \varphi = - \frac{\pi }{3}\)