Cho cơ hệ như hình: lò xo có độ cứng k=100N/m
Câu hỏi :
Cho cơ hệ như hình: lò xo có độ cứng k=100N/m, vật nặng khối lượng m=100g, bề mặt chỉ có ma sát trên đoạn CD, biết CD=1cm và μ=0,5. Ban đầu vật nặng nằm tại vị trí lò xo không biến dạng, truyền cho vật vận tốc ban đầu v0=60π cm/s dọc theo trục của lò xo hướng theo chiều lò xo giãn. Lấy g=10 m/s2. Tốc độ trung bình của vật nặng kể từ thời điểm ban đầu đến khi nó đổi chiều chuyển động lần thứ nhất gần nhất giá trị nào sau đây?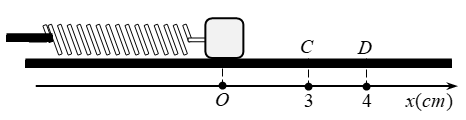
A. 50 cm/s
B. 100 cm/s
C. 150 cm/s
D. 200 cm/s
* Đáp án
B
* Hướng dẫn giải
Ta có:
- k=100N/m; m=100g.
- \(\omega = \sqrt {\frac{k}{m}} = \sqrt {\frac{{100}}{{\left( {{{100.10}^{ - 3}}} \right)}}} = 10\pi \)rad/s → T=0,2s.
Chuyển động của vật kể từ thời điểm ban đầu đến lúc nó đổi chiều chuyển động lần đầu tiên được chia thành các giai đoạn sau:
Giai đoạn 1: Chuyển động từ O đến C
- là dao động điều hòa với biên độ \({A_1} = \frac{{{v_0}}}{\omega } = \frac{{60\pi }}{{10\pi }} = 6\)cm.
- thời gian chuyển động \({t_1} = \frac{T}{{12}} = \frac{{0,2}}{{12}} = \frac{1}{{60}}\)s.
- vận tốc khi vật đến C: \({v_C} = \frac{{\sqrt 3 }}{2}{v_0} = \frac{{\sqrt 3 }}{2}.\left( {60\pi } \right) = 30\sqrt 3 \pi \)cm/s.
Giai đoạn 2: Chuyển động từ C đến D
- là dao động điều hòa chịu thêm tác dụng của ma sát có độ lớn không đổi. Vị trí cân bằng mới lệch khỏi O theo hướng lò xo bị nén một đoạn
\(\begin{array}{l}
\Delta {l_0} = \frac{{\mu mg}}{k} = \frac{{\left( {0,5} \right).\left( {{{100.10}^{ - 3}}} \right).\left( {10} \right)}}{{100}} = 0,5cm\\
\Rightarrow {A_2} = \sqrt {{{\left( {\Delta {l_0} + OC} \right)}^2} + {{\left( {\frac{{{v_C}}}{\omega }} \right)}^2}} = \sqrt {{{\left( {0,5 + 3} \right)}^2} + {{\left( {\frac{{30\sqrt 3 \pi }}{{10\pi }}} \right)}^2}} = 6,265cm
\end{array}\)
- thời gian chuyển động \(\Delta {t_2} = \frac{{\arccos \left( {\frac{{3,5}}{{6,265}}} \right) - \arccos \left( {\frac{{4,5}}{{6,265}}} \right)}}{{{{360}^0}}}.\left( {0,2} \right) = {6,64.10^{ - 3}}\)s.
- vận tốc khi vật đến D: \({v_D} = \omega {A_2}\sqrt {1 - {{\left( {\frac{{\Delta {l_0} + OD}}{{{A_2}}}} \right)}^2}} = \left( {10\pi } \right).\left( {6,265} \right).\sqrt {1 - {{\left( {\frac{{4,5}}{{6,265}}} \right)}^2}} = 136,940\)cm/s.
Giai đoạn 3: Chuyển động từ D đến khi đổi chiều lần đầu tiên
- là dao động điều hòa quanh vị trí lò xo không biến dạng với biên độ
\({A_3} = \sqrt {O{D^2} + {{\left( {\frac{{{v_D}}}{\omega }} \right)}^2}} = \sqrt {{4^2} + {{\left( {\frac{{136,940}}{{10\pi }}} \right)}^2}} = 5,916\)cm.
- thời gian chuyển động
\({t_3} = \frac{{arc\cos \left( {\frac{{OD}}{{{A_3}}}} \right)}}{{{{360}^0}}}T = \frac{{arc\cos \left( {\frac{4}{{5,916}}} \right)}}{{{{360}^0}}}.\left( {0,2} \right) = 0,0264\)s.
→ Tốc độ trung bình
\({v_{tb}} = \frac{S}{t} = \frac{{OC + CD + \left( {{A_3} - OD} \right)}}{{{t_1} + {t_2} + {t_3}}} = \frac{{3 + 1 + \left( {5,916 - 4} \right)}}{{\frac{1}{{60}} + {{6,64.10}^{ - 3}} + 0,0264}} = 119,018\)cm/s.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT QG năm 2021 môn Vật Lý Trường THPT Phạm Văn Chiêu
Copyright © 2021 HOCTAP247
