Hình vẽ bên là đồ thị biễu diễn sự phụ thuộc
Câu hỏi :
Hình vẽ bên là đồ thị biễu diễn sự phụ thuộc của li độ x vào thời gian t của hai dao động điều hòa cùng phương. Dao động của vật là tổng hợp của hai dao động nói trên. Trong 0,20 s đầu tiên kể từ t=0s, tốc độ trung bình của vật bằng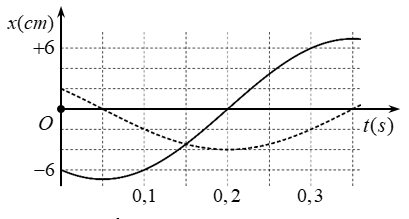
A. 40√3cm/s.
B. 40 cm/s.
C. 20√3cm/s.
D. 20 cm/s.
* Đáp án
B
* Hướng dẫn giải
+ Từ đồ thị, ta thấy rằng dao động thành phần ứng với đường liền nét có phương trình \({x_1} = 4\cos \left( {\frac{{10\pi }}{3}t + \frac{\pi }{3}} \right)\) cm.
+ Thành phần dao động ứng với đường nét đứt. Tại \(t = \frac{T}{{12}} = 0,05\) s đồ thị đi qua vị trí x=-A → tại t=0, thành phần dao động này đi qua vị trí:
\(x = - \frac{{\sqrt 3 }}{2}A = - 6cm \Rightarrow A = 4\sqrt 3 cm\)
\(\begin{array}{l}
{x_2} = 4\sqrt 3 \cos \left( {\frac{{10\pi }}{3}t + \frac{{5\pi }}{6}} \right)cm\\
\Rightarrow x = {x_1} + {x_2} = 8\cos \left( {\frac{{10\pi }}{3}t + \frac{{2\pi }}{3}} \right)cm
\end{array}\)
+ Tại t=0, vật đi qua vị trí x=-4 cm theo chiều âm. Sau khoảng thời gian ∆t=0,2 s ứng với góc quét \(\Delta \varphi = \omega \Delta t = {120^0}\) vật đến vị trí x=-4 cm theo chiều dương.
→ \({v_{tb}} = \frac{{4 + 4}}{{0,2}} = 40cm/s\)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT QG năm 2021 môn Vật Lý Trường THPT Tôn Đức Thắng
Copyright © 2021 HOCTAP247
