Một học sinh xác định điện dung của tụ điện bằng cách đặt điện áp u = U0cosωt
Câu hỏi :
Một học sinh xác định điện dung của tụ điện bằng cách đặt điện áp u = U0cosωt (U0 không đổi, ω = 314 rad/s) vào hai đầu một đoạn mạch gồm tụ điện có điện dung C mắc nối tiếp với biến trở R. Biết \(\frac{1}{{{U^2}}} = \frac{2}{{U_0^2}} + \frac{2}{{U_0^2{\omega ^2}{C^2}}}.\frac{1}{{{R^2}}}\) ; trong đó điện áp U giữa hai đầu R được đo bằng đồng hồ đo điện đa năng hiện số. Dựa vào kết quả thực nghiệm đo được trên hình vẽ, học sinh này tính được giá trị của C là: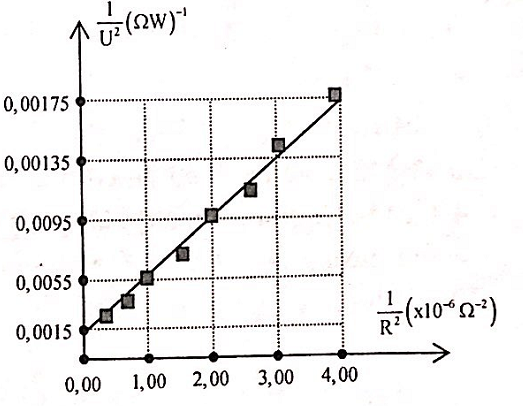
A. 1,95.10-3 F
B. 5,20.10-6 F
C. 5,20.10-3 F
D. 1,95.10-6 F
* Đáp án
D
* Hướng dẫn giải
Từ đồ thị nhận thấy có hai điểm có tọa độ \(\left( {\frac{1}{{{U^2}}} = 0,0055;\frac{1}{{{R^2}}} = {{1.10}^{ - 6}}} \right);\left( {\frac{1}{{{U^2}}} = 0,0095;\frac{1}{{{R^2}}} = {{2.10}^{ - 6}}} \right)\) là kết quả chính xác nhất.
+ Ta có:
\(\left\{ \begin{array}{l}
\frac{1}{{{U^2}}} = 0,0055;\frac{1}{{{R^2}}} = {10^{ - 6}} \Rightarrow 0,0055 = \frac{2}{{U_0^2}}\left( {1 + \frac{1}{{{{314}^2}{C^2}}}{{.10}^{ - 6}}} \right){\kern 1pt} {\rm{ }}\left( 1 \right)\\
\frac{1}{{{U^2}}} = 0,0095;\frac{1}{{{R^2}}} = {2.10^{ - 6}} \Rightarrow 0,0095 = \frac{2}{{U_0^2}}\left( {1 + \frac{1}{{{{314}^2}{C^2}}}{{.2.10}^{ - 6}}} \right){\rm{ }}\left( 2 \right)
\end{array} \right.\)
+ Lấy (2) chia (1), ta có: \(C = {1,95.10^{ - 6}}F\)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT QG năm 2021 môn Vật Lý Trường THPT Ngô Quyền
Copyright © 2021 HOCTAP247
