Một vật dao động diều hòa với phương trình

* Hướng dẫn giải

Chu kì dao động của vật là: T=2π/ω=2(s)

+ Trong một chu kì, khoảng thời gian mà \(\left| v \right| \ge \pi \left( {a - b} \right)\) là 4Δt được biểu diễn như hình.

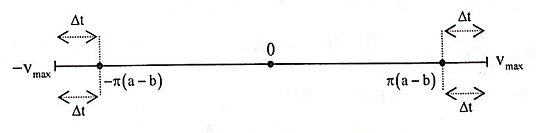
+ Theo đề, ta có: 

\(\begin{array}{l}
4\Delta t = \frac{2}{3} \Rightarrow \Delta t = \frac{2}{{12}}s = \frac{T}{{12}} \Rightarrow \left| v \right| = \frac{{{v_{\max }}\sqrt 3 }}{2}\\
 \Leftrightarrow \pi \left( {a - b} \right) = \frac{{{v_{\max }}\sqrt 3 }}{2} \Leftrightarrow \pi \left( {a - b} \right) = \frac{{\pi A\sqrt 3 }}{2} \Rightarrow a - b = \frac{{A\sqrt 3 }}{2}(1)
\end{array}\)

+ Theo (1) suy ra a > b kết hợp với giả thiết đề bài suy ra thời gian ngắn nhất giữa hai lần liên tiếp vật cách vị trí cân bằng một khoảng bằng a và b được biểu diễn như hình vẽ.

​

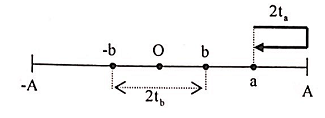
+ Ta có:  

\(\begin{array}{l}
\left\{ \begin{array}{l}
{t_a} = \frac{1}{\omega }\arccos \frac{a}{A} \Rightarrow a = A\cos \left( {\omega .{t_a}} \right)\\
{t_b} = \frac{1}{\omega }\arcsin \frac{b}{A} \Rightarrow b = A\sin \left( {\omega .{t_b}} \right)
\end{array} \right.\\
{t_a} = {t_b} = t \Rightarrow \left\{ \begin{array}{l}
a = A\cos \left( {\omega .t} \right)\\
b = A\sin \left( {\omega .t} \right)
\end{array} \right.\\
 \Rightarrow {\left( {\frac{a}{A}} \right)^2} + {\left( {\frac{b}{A}} \right)^2} = 1 \Rightarrow {a^2} + {b^2} = {A^2}{\left( {b + \frac{{A\sqrt 3 }}{2}} \right)^2} + {b^2} = {A^2}\\
 \Leftrightarrow 2{b^2} + b.A\sqrt 3  - \frac{{{A^2}}}{4} = 0 \Rightarrow b = \left( {\frac{{\sqrt 5  - \sqrt 3 }}{4}} \right)A\\
 \Rightarrow a = b + \frac{{A\sqrt 3 }}{2} = \left( {\frac{{\sqrt 5  + \sqrt 3 }}{4}} \right)A \Rightarrow \frac{a}{b} + \sqrt {15}  = 7,87
\end{array}\)