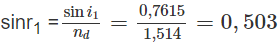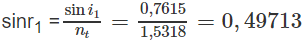Một lăng kính thuỷ tinh có tiết diện thẳng là một tam giác đều

* Hướng dẫn giải

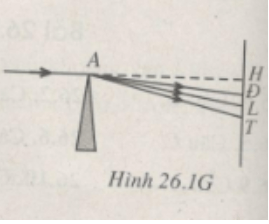
Gọi H là giao điểm của đường kéo dài tia tới với màn ảnh (H.26.1G).

Ta có: AH = 2 m.

Ta hãy tính góc lệch của tia lam.

Vì góc lệch của tia lam là cực tiểu nên

$r_1$ = $r_2$ = A/2 = 30$°$

sin$i_1$ = $n_1$sin$r_1$ = 1,525.0,5 = 0,7615

⇒ $i_1$ = 49,5966$°$ = $i_2$

$D_{lam min}$ = $i_1$ + $i_2$ - A = 39,193$°$

Gọi L là giao điểm của tia lam với màn ảnh, ta có :

HL = AHtan$D_{lam min}$ = 2tan39,193$°$ = 1,631 m

Ta hãy tính góc lệch của tia đỏ.

$r_1$ = 30,199$°$ ; $r_2$ = A - $r_1$ = 60 - 30,199 = 29,801$°$

sin$i_2$ = $n_{đ}$sin$r_2$ = 1,5140. sin29,801$°$ = 0,75244 ⇒ $i_2$ = 48,802$°$

$D_{đ}$ = $i_1$ + $i_2$ - A = 49,5966$°$ + 48,802$°$ - 60$°$ = 38,3986$°$

Gọi Đ là vết của tia đỏ trên màn ảnh, ta có :

HĐ = AH tan$D_{đ}$ = 2.tan38,3986$°$ = 1,585 m

Tương tự, đối với tia tím, ta có :

$r_1$ = 29,810$°$ ; $r_2$ = A - $r_1$ = 60$°$- 29,810$°$ = 30,19$°$

sin$i_2$ = ntsin$r_2$ = 1,5318.sin30,19$°$ = 0,7703 ⇒ $i_2$ = 50,381$°$

$D_t$ = $i_1$ + $i_2$ - A = 49,5966$°$ + 50,381$°$ - 60$°$ = 39,977$°$

Gọi T là vết của tia tím trên màn ảnh, ta có :

HT = AH tan$D_t$ = 2. 0,834 = 1,668 m

Khoảng cách giữa vạch đỏ và vạch lam :

HL - HĐ = 1,631 - 1,585 = 0,046 m = 4,6 cm

Khoảng cách giữa vạch lam và vạch tím :

HT - HL = 1,668 - 1,631 = 0,037 m = 3,7 cm.