Trên mặt thoáng của chất lỏng có hai nguồn A, B cách nhau 4cm

* Hướng dẫn giải

​

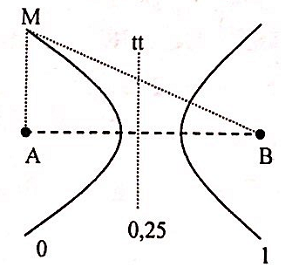
Độ lệch pha của hai sóng do nguồn truyền đến M:

\(\Delta \varphi  = {\varphi _2} - {\varphi _1} + \frac{{2\pi \left( {{d_1} - {d_2}} \right)}}{\lambda } = \frac{\pi }{2} + \frac{{2\pi \left( {{d_1} - {d_2}} \right)}}{\lambda }\) 

+ Để M dao động cực đại thì:

\(\Delta \varphi  = 2k\pi  \Leftrightarrow \frac{\pi }{2} + \frac{{2\pi \left( {{d_1} - {d_2}} \right)}}{\lambda } = 2k\pi  \Rightarrow {d_1} - {d_2} = \left( {k - 0,25} \right)\lambda \) 

+ Xét tại trung trực nên:

\({d_1} = {d_2} \Rightarrow \left( {k - 0,25} \right)\lambda  = 0 \Rightarrow k = 0,25\) 

=> cực đại gần trung trực nhất về phía A ứng với k = 0

\( \Rightarrow {d_{1M}} - {d_{2M}} = \left( {0 - 0,25} \right)\lambda  \Leftrightarrow MA - MB =  - 0,25\)    (1)

+ Vì tam giác MAB vuông ở A nên: \(MB = \sqrt {M{A^2} + A{B^2}} \)    (2)

+ Thay (1) vào (2), ta có: \(MA - \sqrt {M{A^2} + {4^2}}  =  - 0,25 \Rightarrow MA = 31,875\) cm