Việt di chuyển từ điểm A trên đoạn đường có nghe một loa phát thanh

* Hướng dẫn giải

​

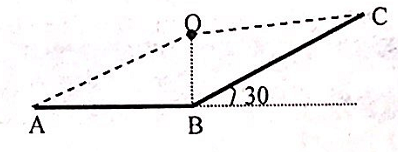
+ Ta có:

\(I = \frac{P}{{4\pi {R^2}}} \Rightarrow \frac{{{I_B}}}{{{I_A}}} = 4 \Leftrightarrow {\left( {\frac{{OA}}{{OB}}} \right)^2} = 4 \Rightarrow OA = 2OB \Rightarrow \left\{ \begin{array}{l}
OB = a\\
OA = 2a
\end{array} \right.\) 

+ Ta có:  

\(\begin{array}{l}
\sin \widehat A = \frac{{OB}}{{OA}} = \frac{1}{2} \Rightarrow \widehat A = 30^\circ \\
 \Rightarrow \tan \widehat A = \frac{{OB}}{{AB}} \Leftrightarrow \tan 30^\circ  = \frac{{OB}}{{12\sqrt 3 }} \Rightarrow OB = 12\left( {{\rm{cm}}} \right)
\end{array}\) 

+ Vì \({I_A} = {I_C} \Leftrightarrow OA = OC = 2a = 24\left( {{\rm{cm}}} \right)\) 

+ Áp dụng định lí hàm có cho tam giác OBC, ta có:

 \(\begin{array}{l}
O{C^2} = O{B^2} + B{C^2} - 2OB.BC.\cos \widehat {OBC}\\
 \Leftrightarrow {24^2} = {12^2} + B{C^2} - 2.12.BC.\cos 60^\circ  \Rightarrow BC = 27,63\left( {{\rm{cm}}} \right)
\end{array}\)