Trong hiện tượng giao thoa sóng nước, hai nguồn A và B cách nhau 10,2cm

* Hướng dẫn giải

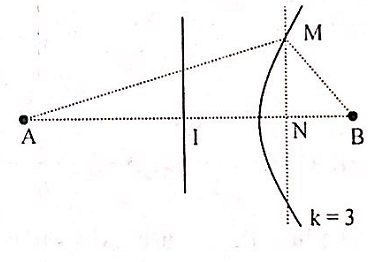
+ Ta có: \(\lambda  = \frac{v}{f} = 2\left( {cm} \right) \Rightarrow {d_{1N}} - {d_{2N}} = 8,2 - 2 = 6,2\left( {cm} \right) = 3,1\lambda \) 

+ Vậy, điểm M gần B nhất khi M thuộc cực đại k = 3

+ Vì M thuộc cực đại k = 3 nên:   

\(\begin{array}{l}
MA - MB = 3\lambda  = 6\left( {cm} \right)\\
\left\{ \begin{array}{l}
MA = \sqrt {A{N^2} + {x^2}}  = \sqrt {{{8,2}^2} + {x^2}} \\
MB = \sqrt {B{N^2} + {x^2}}  = \sqrt {{2^2} + {x^2}} 
\end{array} \right.\\
 \Rightarrow \sqrt {{{8,2}^2} + {x^2}}  - \sqrt {{2^2} + {x^2}}  = 6
\end{array}\)

+ Bấm máy tính giải , ta có: x = 1,1 cm